Горизонты XXI века: математический анализ гипотезы Сингулярности

скачать Автор: Коротаев А. В. - подписаться на статьи автора
Журнал: Историческая психология и социология истории. Том 11, номер 2/ 2018 - подписаться на статьи журнала

DOI: https://doi.org/10.30884/ipsi/2018.02.01

Представление о том, что в ближайшее время нас ждет некая «сингулярность», стало в последнее время популярным, прежде всего благодаря деятельности технического директора Google в области машинного обучения Р. Курцвейла. Показано, что математический анализ приводимого им ряда событий, начинающегося с возникновения нашей Галактики и заканчивающегося расшифровкой кода ДНК, действительно практически идеально описывается (неизвестной самому Курцвейлу) крайне простой математической функцией с сингулярностью в районе 2029 года. Показано также, что составленный в начале 2000-х годов (совершенно независимо от Курцвейла) российским физиком А. Д. Пановым аналогичный временной ряд (начинающийся с возникновения жизни на Земле и заканчивающийся информационной революцией) также практически идеально описывается (не использованной Пановым) математической функцией (крайне сходной с вышеупомянутой) с сингулярностью в районе 2027 года. Отмечено, что эта функция также чрезвычайно сходна с уравнением, открытым в 1960 году Х. фон Ферстером, показавшим в знаменитой статье в журнале “Science”, что оно практически идеально описывает динамику численности населения Земли и характеризуется математической сингулярностью в районе 2027 года. Все это говорит о наличии достаточно строгих глобальных макроэволюционных закономерностей, которые могут удивительно точно описываться крайне простыми математическими функциями. Вместе с тем продемонстрировано, что в районе точки сингулярности нет оснований вслед за Курцвейлом ожидать невиданного (на много порядков) ускорения темпов технологического развития; имеются бóльшие основания интерпретировать эту точку как индикатор зоны перегиба, после прохождения которой темпы глобальной эволюции в долгосрочной перспективе будут систематически замедляться.

Ключевые слова: макроэволюция, глобальная история, Сингулярность, Большая история, биологическая эволюция, социальная эволюция, технологический прогресс, гиперболическое ускорение.

Вопрос о «сингулярности» глобальной (или даже Большой) истории обсуждается в последнее время очень активно (см., например: Назаретян 2013; 2014; 2015а; 2015б; Eden et al. 2012; Shanahan 2015; Callaghan et al. 2017; Nazaretyan 2015; 2016; 2017; 2018). Этот вопрос стал особенно популярным благодаря усилиям Р. Курцвейла, технического директора в области машинного обучения и обработки естественного языка компании Google, в особенности благодаря его книге (Kurzweil 2005), но также и через создание им в 2009 году Университета Сингулярности, активную пиар-кампанию и т. п. В сфере Большой истории [1] внимание к проблеме Сингулярности было привлечено благодаря деятельности таких специалистов в этой области, как А. П. Назаретян (2005; 2009; 2013; 2014; 2015а; 2015б; Балашова и др. 2017; Nazaretyan 2005; 2015; 2016; 2017; 2018), А. Д. Панов (2004; 2005; 2006; 2008; Panov 2005;  2011; 2017) и Г. Д. Снукс (Snooks 2005). В перспективе Большой истории гипотеза Сингулярности может представлять определенный интерес, так как она вроде бы предлагает «научно обоснованную» датировку девятой пороговой вехи Большой истории (Big History Threshold 9) [2]. Попробуем прежде всего разобраться, могут ли математические расчеты даты Сингулярности действительно помочь выявить дату наступления очередной пороговой вехи Большой истории.

Временной ряда Курцвейла – Модиса и математическая сингулярность

Р. Курцвейл одним из первых расположил главные макроэволюционные сдвиги значительной части Большой истории вдоль гиперболической кривой, которая может быть описана уравнением с математической сингулярностью. Например, он приводит следующую диаграмму (см. рис. 1) [3]:

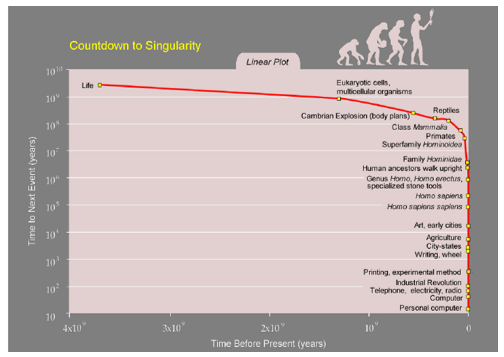
Рис. 1. Обратный отсчет времени до Сингулярности, согласно (Kurzweil 2005: 18)

Однако, как ни удивительно, Курцвейл, по-видимому, не заметил, что кривая на рисунке является гиперболической и описывается уравнением, имеющим самую настоящую математическую сингулярность (более того, значение этой сингулярности, 2029 год, не так далеко от того, что предсказывается самим Курцвейлом). Это объясняется прежде всего некоторыми математическими неточностями, характерными для технического директора Google (достаточно упомянуть, что он упорно называет глобальный паттерн ускорения эволюции экспоненциальным, не обращая внимания на то, что экспоненциальная функция не имеет сингулярности).

Не может не вызвать некоторое удивление и то обстоятельство, что cам Курцвейл знает о понятии математической сингулярности и более или менее точно описывает его. Действительно, на с. 22–23 своего бестселлера он дает довольно точное описание понятия «математическая сингулярность»: «Singularity – это английское слово, означающее уникальное в своем роде событие с крайне специфическими последствиями. Это слово используется математиками для обозначения значения, которое превосходит любое конечное ограничение, такое как взрывообразный рост величины, который возникает при делении константы на переменную, значение которой все больше приближается к нулю. Такая математическая функция никогда не достигает бесконечного значения, поскольку деление на ноль математически “не определено” (это невозможно вычислить). Но значение у превосходит любой возможный конечный предел (приближается к бесконечности), когда знаменатель х стремится к нулю» (Kurzweil 2005: 22–23). Более того, он сопровождает свое описание понятия «математическая сингулярность» вполне адекватным иллюстрирующим графиком (см. рис. 2) (Ibid.: 23). Однако, представив достаточно точное описание понятия «математическая сингулярность», Курцвейл, похоже, теряет интерес к нему, внезапно переключаясь на использование термина «сингулярность» астрофизиками.

Еще один из загадочных аспектов книги Курцвейла заключается в том, что он, похоже, не заметил, что форма гиперболической кривой на его графике «Математическая сингулярность» (см. рис. 2) принципиально идентична (хотя, конечно, повернута на 180 градусов) форме кривой на его графике «Обратный отсчет времени до Сингулярности» (см. рис. 1). Более того, как мы увидим ниже, математическая модель, обеспечивающая наилучшую аппроксимацию кривой типа той, что изображена на рис. 1, в основном идентична гиперболической функции, показанной на рис. 2, т. е. y = k / x. Таким образом, если бы Курцвейл сделал простой математический анализ временного ряда на рис. 1, он бы нашел, что его лучше всего описывает математическое уравнение того самого типа, что он изображает на рис. 2 (с той очень небольшой разницей, что у нас в числителе уравнения оказалось бы 2, а не 1). Более того, он обнаружил бы, что значение математической сингулярности уравнения, лучше всего описывающего кривую на графике «Обратный отсчет времени до Сингулярности» Курцвейла (см. рис. 1), соответствует 2029 году, что не так сильно отличается от 2045 года, предложенного в его книге, и просто идентично дате, предложенной Курцвейлом совсем недавно (см.: Ranj 2016) [4].

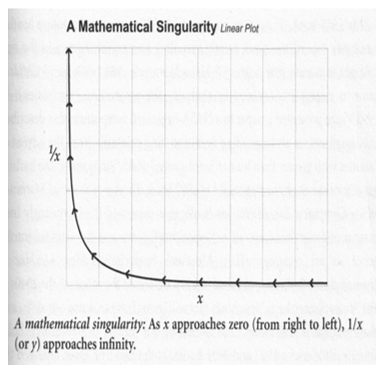
Рис. 2. Пример математической сингулярности (в натуральном масштабе) (Kurzweil 2005: 23)

Преобразование Панова

То, что не было сделано Р. Курцвейлом в 2005 году, было сделано еще в 2003 году А. Д. Пановым [5]. Он проанализировал достаточно похожий временной ряд (построенный, впрочем, на совершенно других источниках) и пришел к очень похожим выводам, но в гораздо более продвинутой форме. Очень важно, что Панов совершил шаг (к которому Курцвейл был очень близок), позволивший ему сделать анализ рассматриваемого временного ряда гораздо более прозрачным, благодаря чему он смог точно рассчитать дату сингулярности.

В книге 2005 года Курцвейл отложил по оси ординат своих диаграмм «время до следующего события», что, на мой взгляд, существенно затруднило их интерпретацию. Вместе с тем в эссе 2001 года при анализе диаграммы с аналогичным временным рядом (источник которого, кстати, не был указан) Курцвейл начал говорить об ускорении «скорости сдвига парадигм» (paradigm shift rate) (Kurzweil 2001: 5), но (что довольно типично для главного инженера Google) почти сразу же переключился на другую тему. Чтобы его диаграммы стали гораздо более понятными, стоило отложить по оси ординат не «время до следующего события», а именно «скорость сдвига парадигм», как это сделал Панов. Действительно, чтобы преобразовать время до следующего «парадигмального сдвига» в скорость сдвига парадигм, нужно было предпринять довольно простое действие: взять один год и разделить его на время до следующего сдвига парадигм; в результате мы получим число парадигмальных сдвигов в год, т. е. именно «скорость сдвига парадигм». Как мы уже говорили, это не было сделано Курцвейлом, но было сделано Пановым, получившим в результате следующие графики (см. рис. 3):

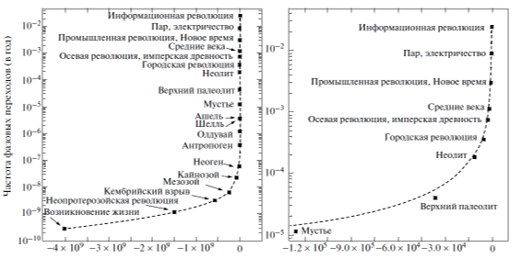
Рис. 3. Динамика скорости глобального макроэволюционного развития, согласно Панову (Назаретян 2015а: 760)

Математическая интерпретация графика Панова намного проще и нагляднее. Заметим, что сам Панов обозначал переменную, нанесенную по оси ординат его графиков, как «частоту фазовых переходов в год». Однако совершенно очевидно, что «фазовый переход» Панова является синонимом «сдвига парадигм» Курцвейла, тогда как «частота фазовых переходов в год» описывает именно «скорость парадигмальных сдвигов» или темпы глобального макроэволюционного развития / темпы роста глобальной сложности. Это преобразование значительно упрощает точное определение картины ускорения темпов глобального макроэволюционного развития.

Временной ряд Курцвейла – Модиса: формальный анализ

Ниже проведен математический анализ временного ряда Курцвейла – Модиса по линии, предложенной Пановым (хотя и с некоторыми нашими модификациями). В дополнение к графику, приведенному нами на рис. 1, Курцвейл публикует две другие версии этого графика в двойной логарифмической шкале (см. рис. 4 и 5):

Рис. 4. Первая версия графика Курцвейла «Обратный отсчет времени до Сингулярности» в двойной логарифмической шкале (Kurzweil 2005: 17)

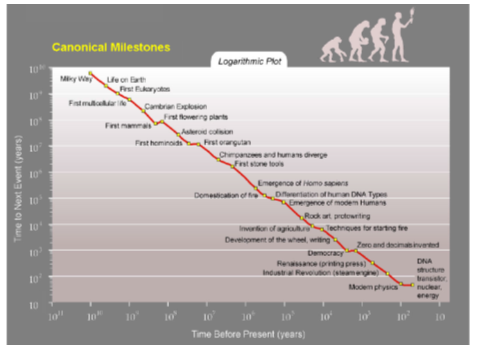
Рис. 5. Вторая версия графика Курцвейла «Обратный отсчет
времени до Сингулярности» («Канонические вехи», Canonical Milestones) в двойной логарифмической шкале (Kurzweil 2005: 20)

Хотя временной ряд на рис. 4 представляется мне несколько более обоснованным, чем тот, который видим на рис. 5, я решил проанализировать временной ряд на рис. 5 по следующей причине. Дело в том, что источник данных для рис. 4 остается для меня совершенно неясным; следовательно, я не вижу способа восстановить соответствующий временной ряд до тех деталей, которые необходимы для его формального математического анализа. Но таких проблем нет с источником данных для рис. 5, поскольку Курцвейл указывает его совершенно четко. Это статья Т. Модиса (Modis 2003), подготовленная, в свою очередь, на основе его предыдущей статьи (Idem 2002). К счастью, Модис публикует все необходимые данные по своему временному ряду, что дает возможность его математически анализировать.

Мы начнем наш анализ с вышеупомянутого преобразования, т. е. заменим «время до следующего события» на «интенсивность парадигмальных сдвигов» ~ «частоту фазовых переходов» ~ «скорость глобального макроэволюционного развития» ~ «скорость роста глобальной сложности». Результат выглядит следующим образом (см. рис. 6):

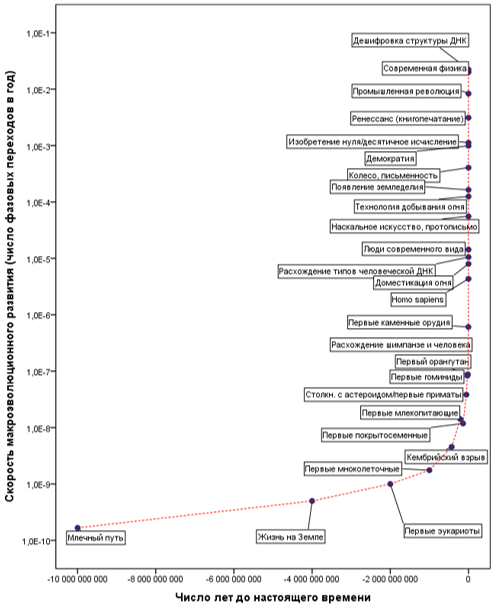
Рис. 6. График Курцвейла «Канонические вехи», трансформированный с использованием преобразования Панова
(с логарифмической шкалой по оси ординат)

С использованием же той техники, которая была применена Курцвейлом при построении графика «Обратный отсчет времени до Сингулярности» (см. рис. 1), мы получим для анализируемого нами временного ряда следующий график (см. рис. 7):

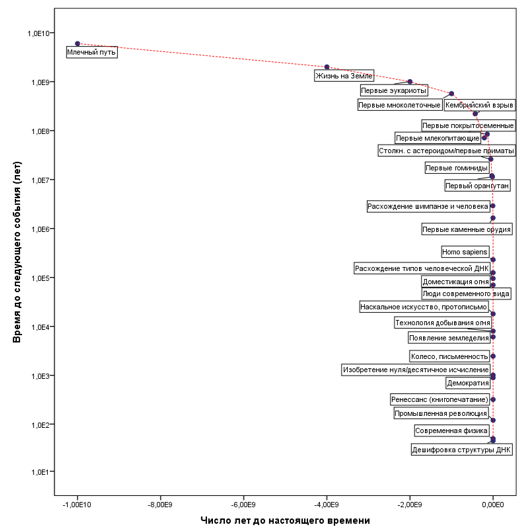
Рис. 7. График Курцвейла «Канонические вехи» с логарифмической шкалой по оси ординат

На рис. 8 видно, что один график является зеркальным отражением другого:

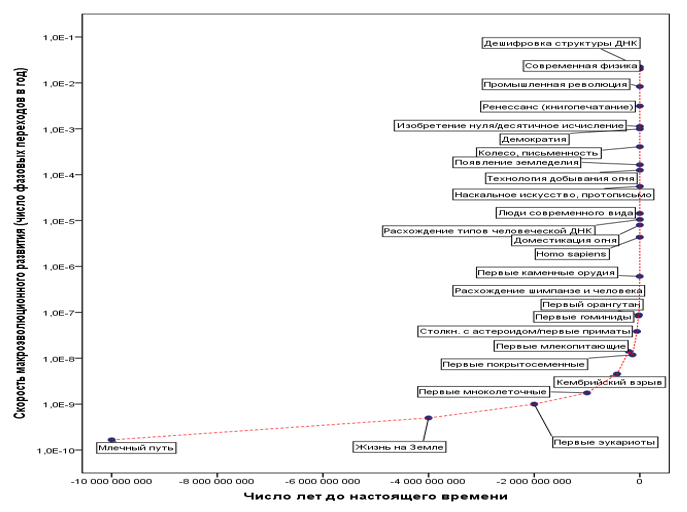
а)

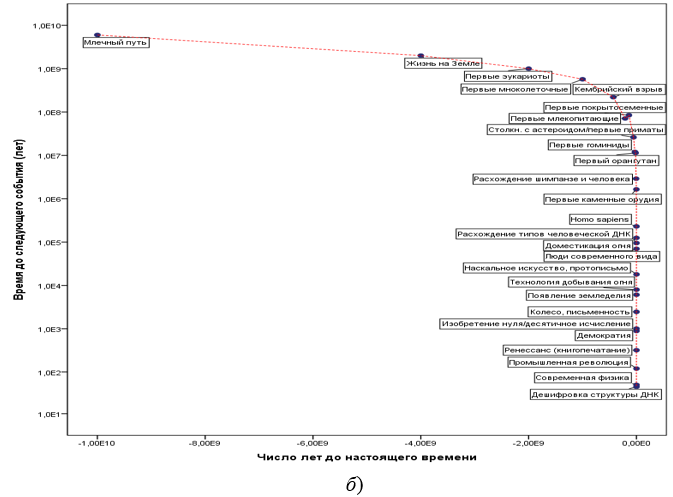
Рис. 8. График по Панову (a) является зеркальным отражением курцвейловского (б)

Хорошо видно, что кривая на рис. 7 (= рис. 8а) практически идентична гиперболической кривой на рис. 2, иллюстрирующей математическую функцию с сингулярностью. На следующем шаге отложим по оси абсцисс время до Сингулярности, а по оси ординат – скорость глобальной макроэволюции (число фазовых переходов в единицу времени) и вычислим дату сингулярности, получив (методом наименьших квадратов) такую гиперболическую кривую, которая наиболее точно описывает анализируемый нами временной ряд. Результаты этого анализа представлены на рис. 9 (как уже упоминалось выше, наш математический анализ определил дату сингулярности для этого временного ряда как 2029 год н. э.).

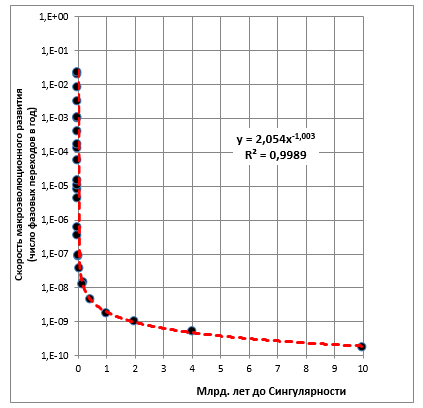
Рис. 9. Диаграмма рассеивания (с логарифмической шкалой по оси ординат) для точек фазовых переходов из списка Модиса – Курцвейла
с добавленной линией степенной регрессии с датой Сингулярности, идентифицированной методом наименьших квадратов в районе 2029 года н. э.

На рис. 10 тот же самый график представлен в двойной логарифмической шкале:

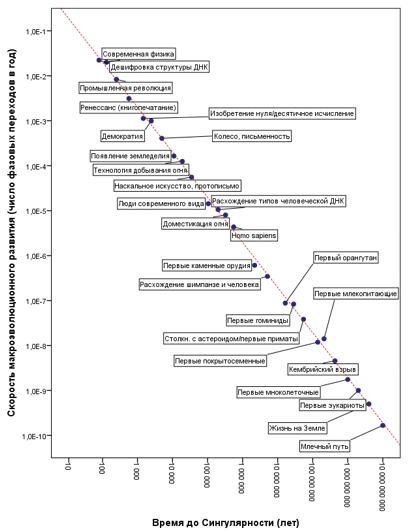
Рис. 10. Диаграмма рассеивания (в двойной логарифмической шкале) для точек фазовых переходов из списка Модиса – Курцвейла
с наложенной линией степенной регрессии с датой Сингулярности, идентифицированной методом наименьших квадратов
в районе 2029 года н. э.

Теперь проанализируем полученные нами результаты. Как видим, временной ряд Модиса – Курцвейла с чрезвычайно высокой точностью описывается с помощью математической функции типа y = k / x, имеющей откровенно выраженную математическую сингулярность, которую Курцвейл вполне точно охарактеризовал на с. 22–23 своей книги, не обратив внимания на ее релевантность для математического описания временного ряда «Обратный отсчет времени до сингулярности», представленного им всего за несколько страниц до этого (с. 17–20). Действительно, наша степенная регрессия для рассматриваемого нами курцвейловского временного ряда «Обратный отсчет времени до сингулярности» определила следующее наилучшим образом подходящее уравнение, описывающее этот временной ряд с почти идеальной точностью (R² = 0,999(!)):

,

(1)

где y – скорость роста глобальной сложности (число фазовых переходов за единицу времени), x – время до Сингулярности, а 2,054 и 1,003 – константы.

Отметим, что показатель степени знаменателя (1,003) лишь в пренебрежимо малой степени отличается от «1» (полностью в пределах погрешности); таким образом, имеются все основания использовать это уравнение в следующей упрощенной форме:

,

(2)

где y – скорость роста глобальной сложности (число фазовых переходов за единицу времени), x – время до Сингулярности, а 2,054 – константа. Таким образом, временной ряд Модиса – Курцвейла может быть с удивительно высокой точностью математически описан при помощи той самой простой гиперболической функции, которую Курцвейл представляет на с. 22–23 своей книги – с той лишь разницей, что в знаменателе правой части этого уравнения находится 2 (а не 1).

Экспоненциальная и гиперболическая формулы глобального ускорения

Особо стоит подчеркнуть, что проведенный нами анализ достаточно строго демонстрирует: паттерн ускорения роста глобальной сложности, прослеживаемый во временном ряду Модиса – Курцвейла, является НЕ экспоненциальным (как это утверждает Курцвейл), а гиперэкспоненциальным, или, если быть более точными, гиперболическим (см. рис. 11).

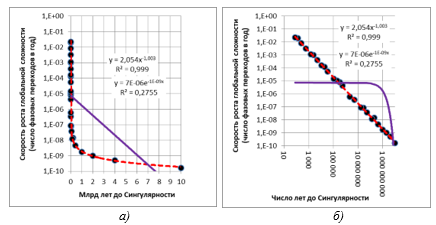
Рис. 11. Диаграмма рассеивания для точек фазовых переходов
из списка Модиса – Курцвейла с наложенными линиями степенной/
гиперболической и экспоненциальной регрессии: a) с логарифмической шкалой по оси ординат; б) в двойной логарифмической шкале.
Сплошные регрессионные линии были сгенерированы экспоненциальной моделью, продемонстрировавшей (методом наименьших квадратов) наилучшее соответствие эмпирическим оценкам,
пунктирные линии – гиперболическим уравнением

Стоит вспомнить, что при использовании логарифмической шкалы по оси ординат экспоненциальная кривая выглядит как прямая линия (в то время как гиперболическая линия кажется похожей на экспоненциальную кривую). Вместе с тем в двойной логарифмической шкале гиперболическая кривая выглядит как прямая линия, в то время как экспоненциальная кривая оказывается похожей на перевернутую экспоненциальную линию. Таким образом, как показывает рис. 11, Р. Курцвейл не вполне прав, утверждая, что глобальное макроэволюционное развитие ускорялось экспоненциально, демонстрируя, что это ускорение было отнюдь не экспоненциальным, а гиперболическим.

Формула ускорения глобального макроэволюционного развития по временному ряду Модиса – Курцвейла

Чтобы сделать рассматриваемую модель ускорения более понятной, произведем небольшое преобразование уравнения (2). Напомним, что это уравнение представляет собой немного упрощенную версию уравнения (1), использованного для генерирования гиперболических кривых на рис. 11.

Конечно, x (время до Сингулярности) на момент времени t равняется t* – t, где t* – это дата Сингулярности. Следовательно,

х = t* – t.

С учетом данного обстоятельства уравнение (2) может быть переписано следующим образом:

где y – это скорость глобального макроэволюционного развития / темпы роста глобальной сложности на момент времени t, t* – это дата Сингулярности, а 2,054 – константа.

Наконец, вспомним, что регрессионный анализ трансформированного временного ряда Модиса – Курцвейла с использованием метода наименьших квадратов позволил нам идентифицировать дату сингулярности как 2029 год н. э. С учетом этого обстоятельства уравнение (3) может быть записано следующим образом:

При этом в общем виде данная модель выглядит так:

где C и t* – константы.

Несмотря на небольшое упрощение (в виде округления показателя степени в знаменателе до 1), уравнение (4) генерирует такие кривые, которые демонстрируют чрезвычайно высокое (R² =
= 0,999(!)) соответствие эмпирическим оценкам паттерна гиперболического ускорения роста глобальной сложности.

Кривая, сгенерированная этим чрезвычайно простым уравнением, неожиданно точно описывает паттерн гиперболического ускорения темпов планетарного макроэволюционного развития на протяжении миллиардов лет (см. рис. 12).

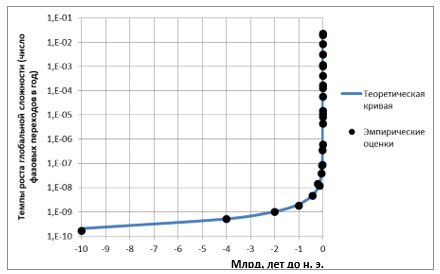
Рис. 12. Корреляция между эмпирическими оценками темпов роста
глобальной сложности и теоретической кривой, сгенерированной
гиперболическим уравнением y_t = 2,054 / (2029 – t),
10 млрд. лет до н. э. – 2000 год н. э.,
с логарифмической шкалой по оси ординат

Как видим, простое гиперболическое уравнение y_t = 2,054 / / (2029 – t) описывает наблюдавшееся до самого последнего времени ускорение темпов глобального макроэволюционного развития удивительно точным образом для всех основных эр глобальной истории.

Собственно говоря, модель (4) имеет достаточно простой «физический смысл». Действительно, подсчитаем скорость глобального макроэволюционного развития примерно за 200 лет до Сингулярности (т. е. около 1829 года), пользуясь еще более упрощенным видом уравнения (4) (y_t = 2 / (2029 – t)): y₁₈₂₉ = 2 / (2029 –  1829) = 2 / 200 = 1 / 100. Таким образом, мы получаем следующий результат: около 1800 года характерная скорость глобального макроэволюционного развития составляла порядка одного фазового перехода (типа промышленной революции) за 100 лет – т. е. глобальное развитие шло в масштабе веков.

Тот же самый подсчет для временной точки примерно за 2000 лет до Сингулярности (≈ до настоящего времени) – около 1 года н. э. – в районе 29 года даст следующий результат: y₂₉ = 2 / (2029 – 29) = 2 / 2000 = 1 / 1000 – таким образом, в эту эпоху макроэволюционные фазовые переходы (типа фазового перехода Осевого времени) имели тенденцию происходить в масштабе один переход за тысячелетие, т. е. в масштабе тысячелетий. Таким образом, в районе 18 тыс. до н. э. мы обнаружим, что планетарное макроэволюционное развитие шло в масштабе десятков тысяч лет, около 200 тыс. лет назад до настоящего времени – в масштабе сотен тысяч лет (около одного фазового перехода за сто тысяч лет), около 2 млн. лет назад – в масштабе миллионов лет, около 20 млн. лет назад – в масштабе десятков миллионов лет, около 200 млн. лет назад – в масштабе сотен миллионов лет, а около 2 млрд. лет назад – в масштабе миллиардов лет (т. е. около одного планетарного макроэволюционного фазового перехода за миллиард лет). Другими словами, с каждым уменьшением времени до настоящего момента (≈ до Сингулярности) на порядок (с 2 млрд. лет назад до 200 млн. лет назад, с 200 млн. лет назад до 20 млн. лет назад, с 20 млн. лет назад до 2 млн. лет назад и т. д.) темпы глобального макроэволюционного развития (~ темпы роста глобальной сложности) всякий раз увеличивались именно на порядок. И лично мне такой паттерн ускорения представляется очень похожим на реально наблюдавшийся.

Здесь также стоит вспомнить, что алгебраическое уравнение типа (5) может рассматриваться как решение следующего дифференциального уравнения:

(6)

(см., например: Korotayev, Malkov, Khaltourina 2006a: 118–120).

Следовательно, формула ускорения, подразумеваемая уравнением (4), может быть выражена следующим образом:

(7)

Вербально общая формула ускорения планетарной макроэволюции, которая столь точно описывает ряд «скачков (в уровне) сложности» [6] Модиса – Курцвейла при помощи уравнений (4)/(5), может быть сформулирована следующим образом: увеличение темпов макроэволюционного развития в a раз сопровождается увеличением скорости роста (т. е. ускорения) темпов макроэволюционного развития в a² раз; так, двукратное увеличение темпов макроэволюционного развития в тенденции сопровождается четырехкратным увеличением скорости роста (т. е. ускорения) темпов макроэволюционного развития; десятикратное увеличение темпов макроэволюционного развития в тенденции сопровождается стократным ускорением роста темпов макроэволюционного развития; и т. д.

Теперь используем ту же самую методику для формального анализа временного ряда глобальных макроэволюционных фазовых переходов / «биосферных революций», идентифицированного Пановым (2004; 2005; 2006; 2008; Panov 2005; 2011; 2017). Однако прежде чем мы проведем этот анализ, представляется целесообразным разобрать несколько существенных моментов.

Временные ряды Модиса – Курцвейла и Панова: внешний сравнительный анализ

Т. Модис и А. Д. Панов провели идентификацию своих временных рядов полностью независимо друг от друга. Как свидетельствует мое личное общение с обоими авторами, ни один из них даже не догадывался, что практически в то же самое время [7] на другом конце Европы другой человек занимался идентификацией очень похожего временного ряда (Панов работал и работает в Москве, а Модис – в Женеве). Как мы увидим ниже, они опирались на совершенно различные источники, и неудивительно, что полученные ими временные ряды оказались совсем не идентичными.

Действительно, временной ряд Модиса (Modis 2003), который стоит за курцвейловским графиком «Канонические вехи» (Kurzweil 2005: 20), выглядит следующим образом (мы воспроизводим его ниже в том виде, как он был опубликован в [Modis 2003]), так как именно на эту версию ряда опирался Курцвейл при создании своего графика и именно эта версия ряда была выше проанализирована математически; мы, однако, время от времени уточняем некоторые детали по более академическому описанию данного ряда из [Idem 2002]):

1. Возникновение Млечного Пути, первые звезды – 10 млрд. лет назад [8].

2. Возникновение жизни на Земле, формирование Солнечной системы и Земли, древнейшие скалы – 4 млрд. лет назад.

3. Появление эукариот, «изобретение» полового размножения (микроорганизмами), атмосферный кислород, древнейшие фотосинтезирующие растения, возникновение тектоники плит – 2 млрд. лет назад.

4. Первые многоклеточные, губки, водоросли, протисты – 1 млрд. лет назад.

5. Кембрийский взрыв / беспозвоночные / позвоночные, pастения колонизируют сушу, первые деревья, рептилии, насекомые, амфибии – 430 млн. лет назад.

6. Первые млекопитающие, первые птицы, первые динозавры – 210 млн. лет назад.

7. Первые покрытосеменные, древнейшие остатки цветковых растений – 139 млн. лет назад.

8. Первые приматы / столкновение с астероидом / массовое вымирание (включая динозавров) – 54,6 млн. лет назад.

9. Первые человекообразные обезьяны, первые гоминиды – 28,5 млн. лет назад.

10. Первый орангутан, проконсул – 16,5 млн. лет назад.

11. Расхождение предков шимпанзе и человека, самые ранние свидетельства прямохождения у гоминид – 5,1 млн. лет назад.

12. Первые каменные орудия, Homo erectus – 2,2 млн. лет назад.

13. Возникновение Homo sapiens – 555 тыс. лет назад.

14. Доместикация огня / Homo heidelbergensis – 325 тыс. лет назад.

15. Расхождение типов человеческой ДНК – 200 тыс. лет назад.

16. Люди современного вида / древнейшие погребения – 105 700 лет назад.

17. Наскальное искусство, протописьмо – 35 800 лет назад.

18. Технология добывания огня – 19 200 лет назад.

19. Появление земледелия – 11 тыс. лет назад.

20. Изобретение колеса / письмо / древние империи / большие цивилизации / Египет / Месопотамия – 4907 лет назад.

21. Демократия / города-государства / древние греки / Будда (≈ Осевое время) – 2437 лет назад.

22. Изобретение нуля и десятичного исчисления, падение Рима, исламские завоевания – 1440 лет назад.

23. Ренессанс (книгопечатание) / открытие Нового Света / научный метод – 539 лет назад.

24. Промышленная революция (паровой двигатель) / политические революции (Франция, США) – 225 лет назад.

25. Современная физика / радио / электричество / автомобиль / аэроплан – 100 лет назад.

26. Дешифровка структуры ДНК / изобретение транзистора / ядерная энергия / Вторая мировая война / холодная война / спут-ник – 50 лет назад.

27. Интернет / расшифровка генома человека – 5 лет назад.

Отметим, что сам Модис заявляет: «…настоящее время приравнивается здесь к 2000 г. н. э.» (Modis 2003: 31). Действительно, это, вне всякого сомнения, имеет смысл по отношению к вехам (24)–(27) из списка Модиса – Курцвейла. Вместе с тем имеются некоторые основания предполагать, что Модис начал составлять первые варианты своего списка за несколько лет до 2000 года и, по всей видимости, не привел в своей публикации 2003 года некоторые старые датировки вех в соответствие с новой условной датой «настоящего времени», установленной на точку 2000 года н. э. Иначе трудно понять датировки им вех (20), (21) и (23).

Т. Модис (Idem 2002: 393–401) дает список научных публикаций, на которые опирался при идентификации своего временного ряда. А. Д. Панов при идентификации своего временного ряда опирался на другие публикации [9] (см. табл. 1):

Таблица 1

Сопоставление источников, использованных Т. Модисом
(Modis 2002; 2003) и А. Д. Пановым (2005) для составления их списков фазовых переходов / «биосферных революций» / «канонических вех» / «эволюционных поворотных точек» / «скачков сложности»

Источники, использованные Модисом для идентификации списка фазовых переходов / «скачков сложности», опубликованного в (Modis 2002; 2003)

Источники, использованные Пановым для идентификации списка фазовых переходов / «биосферных революций», изданного в первой полностью академической публикации его результатов (Панов 2005)

1) Barrow, Silk 1980; 2) Burenhult 1993; 3) Heidmann 1989; 4) Johanson, Edgar 1996; 5) Sagan 1989; 6) Schopf 1991. К этому списку Т. Модис добавляет: 7) Timeline of the Universe (Ame- rican Museum of Natural History, Central Park West at 79th Street, New York); 8) Encyclopedia Britannica; 9) The Web Site of the Educational Resources in Astronomy and Planetary Science (ERAPS), University of Arizona; 10) Private Communication, Paul D. Boyer, Biochemist. Nobel Prize 1997. Dec 27, 2000; 11) A Timeline for Major Events in the History of Life on Earth as Given by David R. Nelson, Department of Biochemistry at the University of Memphis, Tennessee (http://drnelson. utmem.edu/evolution2.html)

Работы российских ученых, опубликованные на русском языке: 1) Борисковский 1970; 2) Он же 1974a; 3) Он же 1974б; 4) Он же 1978; 5) Дьяконов 1994; 6) Федонкин 2003; 7) Галимов 2001; 8) Капица 1996; 9) Келлер 1975; 10) Лопатин 1983; 11) Муратов, Вахрамеев 1974; 12) Назаретян 2004; 13) Розанов 1986; 14) Он же 2003; 15) Розанов, Заварзин 1997; 16) Шанцер 1973; 17) Заварзин 2003; 18) Зайцев 2001. Работы западных ученых, переведенные на русский язык: 1) Антисери, Реале 2001; 2) Биган 2004; 3) Кэрролл 1992; 4) Он же 1993a; 5) Он же 1993б; 6) Фоули 1990; 7) Ясперс 1991; 8) Кринг, Дурда 2004; 9) Вонг 2003. Оригинальные публикации западных ученых на английском языке: 1) Alvarez et al. 1980; 2) Orgel 1998; 3) Wood 1992

Как видим, нет ни одной публикации, на которую опирались бы одновременно и Модис (Modis 2002; 2003), и Панов (2004; 2005), когда они составляли свои списки «канонических вех» / «биосферных революций». Списки использованных ими источников различаются на 100 %. Более того, исследователи в основном опирались на источники, принадлежащие к разным научным традициям. Действительно, Т. Модис опирался исключительно на работы западных ученых, опубликованные на английском языке. В разительном контрасте с этим из 30 источников, использованных А. Д. Пановым (2005), 18 представляют собой работы российских исследователей, опубликованные в России на русском языке, девять – это работы западных ученых, переведенные на русский язык и изданные в России, и лишь три – оригинальные работы западных исследователей на английском языке. В свете этого вряд ли у кого-то вызовет удивление то, что список фазовых переходов Панова (Там же: 124–127) оказался ни в коем случае не идентичным списку Модиса [10]:

«0. Возникновение жизни на Земле – около 4 × 10⁹ лет назад (Orgel 1998; Розанов, Заварзин 1997; Розанов 2003; Федонкин 2003). Жизнь возникает в форме примитивных безъядерных одноклеточных организмов – прокариот (и, возможно, вирусов [Галимов 2001]). После возникновения жизни приблизительно в течение 2–2,5 млрд. лет эволюция протекала, по-видимому, без существенных потрясений, при этом главным системообразующим фактором биосферы была прокариотная фауна. Это видно, в частности, по монотонному росту скорости отложения горючих ископаемых (седиментогенез) вплоть до достижения максимума 2,0–1,5 млрд. лет назад (Лопатин 1983). Однако задолго до конца прокариотной эры возникли первые эукариоты и, возможно, даже примитивные многоклеточные организмы (Розанов 2003; Федонкин 2003). Специально отмечается (Федонкин 2003), что эукариоты не играли заметной роли в глобальных биохимических циклах вплоть до кислородного кризиса около 1,5 млрд. лет назад (см. ниже). Эукариотная фауна на фоне прокариотной существовала в форме избыточного внутреннего разнообразия.

1. Кислородный кризис или неопротерозойская революция – 1,5 × 10⁹ лет назад (Федонкин 2003; Лопатин 1983; Розанов 2003; Заварзин 2003). Цианобактерии обогатили первоначально восстановительную атмосферу Земли кислородом, который был сильным ядом для анаэробных прокариот. Анаэробные организмы стали вымирать, что видно, в частности, по резкому замедлению седиментогенеза в этот период (Лопатин 1983; Розанов, Заварзин 1997). Кислородный кризис – типичный пример эндо-экзогенного кризиса и первый глобальный экологический кризис в истории Земли. На смену анаэробным прокариотам пришли аэробные формы жизни, которые представлены в основном как одноклеточными, так и многоклеточными эукариотами. По разным данным, это событие имело место от 2,0 до 1,0 млрд. лет назад, но при этом фактически подразумеваются разные фазы этого перехода. От пика революции нас отделяет приблизительно 1,5 млрд. лет.

2. Кембрийский взрыв – 590–510 × 10⁶ лет назад (Келлер 1975; Розанов 1986; Кэрролл 1992). В течение нескольких десятков миллионов лет возникают практически все современные филогенетические стволы многоклеточных, включая позвоночных (Кэрролл 1992: 37). Кембрийский взрыв совпадает с началом палеозойской эры. В течение палеозоя жизнь постепенно выходила на сушу и осваивала ее. Уже в кембрии обнаружены первые попытки выхода беспозвоночных на сушу (Федонкин 2003). Палеозойская эра заканчивается господством на суше земноводных, чрезвычайно разнообразных и часто гигантских (Кэрролл 1992), среди растений – хвощей, плаунов и папоротников. За несколько десятков миллионов лет до окончания палеозоя возникают первые пресмыкающиеся (избыточное разнообразие), которые становятся системообразующим фактором следующей фазы развития планетарной системы.

3. Начало мезозойской эры, революция пресмыкающихся – 235 × 10⁶ лет назад (Кэрролл 1992; Муратов, Вахрамеев 1974; Кэрролл 1993а). Внезапно и быстро вымирают практически все отряды палеозойских земноводных (Кэрролл 1992: 192), лидерство на суше переходит к пресмыкающимся – сначала звероподобным и зверозубым ящерам, потом к динозаврам (Он же 1993а). В мире растений начинают господствовать голосеменные (хвойные, гинкговые и др.). Уже в середине мезозоя появляются первые млекопитающие, но в экосистемах они играют подчиненную роль (избыточное разнообразие).

4. Начало кайнозойской эры, революция млекопитающих – 66 × 10⁶ лет назад (Шанцер 1973; Кэрролл 1993а; 1993б). Полностью вымирают динозавры, на суше – гигантский всплеск разнообразия млекопитающих, в воздухе господствуют птицы, среди растений голосеменные вытесняются покрытосеменными (цветковыми). Предположение о том, что вымирание динозавров вызвано исключительно последствиями падения гигантского метеорита, образовавшего кратер Чикулуб (Alvarez et al. 1980; Кринг, Дурда 2004), вызывает серьезную критику, так как вымирание динозавров длилось 1–2 млн. лет, а пыль и сажа могли держаться в атмосфере максимум несколько месяцев (Кэрролл 1993а), при этом длительных глобальных климатических изменений не отмечается.

5. Начало неогена – 25–20 × 10⁶ лет назад (Шанцер 1973; Кэрролл 1993б; Биган 2004) – сопровождается резким обновлением фауны на территории Европы; флора и фауна приобретают практически современный вид. Возникают гоминоиды – человекообразные обезьяны, причем это событие имеет характер сильнейшего эволюционного взрыва. Между 22 и 17 млн. лет назад Африку населяли не менее 14 родов гоминоидов, что составляет десятки видов (Биган 2004) – много больше, чем сейчас.

6. Начало четвертичного периода (антропоген) – 4,4 × 10⁶ лет назад (Биган 2004; Фоули 1990; Wood 1992). Первые примитивные люди (гоминиды) отделяются от обезьяноподобных (гоминоидов). Подобно началу неогена, начало антропогена сопровождалось всплеском разнообразия Homo (Wood 1992). Далее следует несколько событий, имеющих, возможно, не столько биологичес кий, сколько социальный характер (см. обсуждение в конце данного раздела). Периоды различаются по характеру обработки орудий труда людьми каменного века. Существующая традиция, отраженная и в энциклопедиях, выделяет последовательность эпох: олдувай – шелль – ашель – мустье.

7. Олдувай, палеолитическая революция – 2,0–1,6 × 10⁶ лет назад (Борисковский 1974а). Появление первых очень грубо обработанных каменных орудий труда – так называемых чопперов. Галечные культуры, Homo habilis.

8. Шелль – 0,7–0,6 × 10⁶ лет назад (Он же 1978). Овладение огнем, топоровидные орудия с поперечным лезвием (кливеры), грубые рубила. Основной носитель культуры – Homo erectus.

9. Ашель – 0,4 × 10⁶ лет назад (Он же 1970) – характеризуется стандартизированными овальными, треугольными, круглыми и другими симметричными рубилами. Основной представитель по-прежнему Homo erectus. На фоне ашельской культуры появляется неандерталец (Homo sapiens neandertalensis) (Борисковский 1970) и около 160 тыс. лет назад – очень близкий вид Homo sapiens sapiens (Вонг 2003). Однако, по-видимому, ни тот ни другой не играют пока существенной роли в планетарной системе (избыточное разнообразие).

10. Мустье (культурная революция неандертальцев) – 150–100 тыс. лет назад (Назаретян 2004; Борисковский 1974б). Лидером планетарной системы становится неандерталец. Каменные и костяные орудия тонкой обработки – скребла, остроконечники, сверла, ножи. Жилища из костей мамонта и шкур. Захоронение мертвых (примитивные религии). Homo sapiens sapiens по-прежнему не имеет существенного значения в планетарной системе (Назаретян 2004).

11. Верхнепалеолитическая революция (культурная революция кроманьонцев) – 30 тыс. лет назад (Назаретян 2004; Дьяконов 1994). Вымирают неандертальцы, носителем культуры становится человек современного вида Homo sapiens sapiens. Многократно возросла продуктивность использования каменного сырья, заметно усовершенствовались знаковые системы коммуникации. Значительное развитие охотничьей автоматики (копья, ловушки), широкое распространение искусства (наскальные рисунки).

12. Неолитическая революция – 12–9 тыс. лет назад (Назаретян 2004; Дьяконов 1994). В конце верхнего палеолита развитие охотничьих технологий привело к истреблению популяций и целых видов животных, что подорвало пищевые ресурсы палеолитического общества и привело к ужесточению межплеменной конкуренции. Ответом на кризис был переход от присваивающего (охота, собирательство) к производящему (земледелие, скотоводство) хозяйству и смена нормативного геноцида зачаточными формами коллективной эксплуатации (Назаретян 2004). Уже в неолите появляются предки городов, такие как Чатал-Хююк (7–4-е тыс. до н. э.), Иерихон (7-е тыс. до н. э.) (Дьяконов 1994). Однако на этом этапе они еще не являются существенным системообразующим фактором (Там же).

13. Городская революция, начало Древнего мира – 4–3-е тыс. до н. э. (Назаретян 2004; Дьяконов 1994). Массовое распространение крупных человеческих агломераций, возникновение письменности, первых правовых документов, настоящей бюрократии и классового общества, появление ремесел. Революция последовала за распространением бронзовых орудий, демографическим взрывом и обострением конкуренции за плодородные земли.

14. Железный век, эпоха империй, революция Осевого времени – 800–500 лет до н. э. (Ясперс 1991; Назаретян 2004; Дьяконов 1994; Зайцев 2001). Возникновение технологии получения железа около 1000–900 лет до н. э. привело к тому, что оружие стало намного более дешевым, легким, эффективным, а войны – более кровопролитными. Ответом на этот кризис техно-гуманитарного баланса было, во-первых, объединение мелких государств в более крупные образования – империи, и, во-вторых, авторитарное мифологическое мышление стало вытесняться личностным. Личность начала восприниматься как суверенный носитель морального выбора. Это привело к практически одновременному появлению в разных местах Земли мыслителей и полководцев нового типа – таких как Заратустра, иудейские пророки, Сократ, Будда, Конфуций (Ясперс 1991) и др. – и к культурному взрыву Античности (Зайцев 2001).

15. Гибель Древнего мира, начало Средневековья – 400–630 годы (здесь и далее – новой эры) (Дьяконов 1994). Начало перехода я условно связываю с деятельностью Святого Августина и осуждением пелагианства на Карфагенском соборе в 417 году, что означало конец эллинистической философии (Антисери, Реале 2001), а конец перехода – с деятельностью пророка Мухаммеда (570–632). Основное содержание перехода – кризис и гибель Римской империи (Древнего мира) с последующим распространением феодальных государств и княжеств при ведущей роли мировых тоталитарных религий (но, конечно, не сводится только к этому).

16. Первая промышленная революция – 1450–1550 годы (Капица 1996; Назаретян 2004; Дьяконов 1994). В терминологии И. М. Дьяконова (1994) – начало стабильно-абсолютистского постсредневековья. Возникновение промышленного производства (мануфактуры), Великие географические открытия, возникновение книгопечатания и культурный переворот Нового времени.

17. Вторая промышленная революция – 1830–1840 годы (Капица 1996; Дьяконов 1994). Возникновение механизированного производства, эпоха пара и электричества. Начало глобализации в области информации – в 1831 году изобретен телеграф. В культурной области начинает формироваться устойчивое негативное отношение к войне как к средству решения политических вопросов
(Л. Толстой и др.).

18. Информационная революция – 1950 год (Капица 1996; Назаретян 2004; Дьяконов 1994). Переход промышленно развитых стран в постиндустриальную эпоху, когда большая часть населения занята не в материальном производстве, а в сфере обслуживания и в переработке информации. Распространение компьютеров и автоматизированных баз данных. Войны между промышленно развитыми супердержавами вытесняются в виртуальную область, принимая форму холодной войны (изменение уровня техно-гуманитарного баланса).

19. Кризис и распад социалистического лагеря, информационная глобализация – 1991 год. Распад мировой системы тоталитарной плановой экономики, резкое снижение уровня глобального военного противостояния, становление мировой сети Интернет, означающее завершение информационной глобализации. Данные события пока отнюдь не всегда трактуются как революция, но, как будет видно, по некоторым чисто формальным признакам они имеют тот же статус, что и предыдущие» (Панов 2005: 124–127).

Отметим, что последняя точка данных (19) отсутствует на приводимых ниже графиках, но она была использована для оценки скорости глобального макроэволюционного развития для точки данных (18). В свете вышеописанного радикального различия в источниковых базах Модиса и Панова, а также полной независимости проводившихся ими исследований друг от друга вряд ли может вызвать удивление то, что пановский список «биосферных революций» очень значительно отличается от ряда «канонических вех» Модиса – Курцвейла:

1. Список Модиса – Курцвейла содержит 27 «канонических вех», в то время как пановский ряд включает лишь 20 «биосферных революций». Таким образом, как минимум 7 вех Модиса – Курцвейла не имеют никаких параллелей в ряду Панова.

2. Есть лишь одна веха, для которой и Модис, и Панов имеют полностью идентичные название и датировку (Модис – Курцвейл 2 = Панов 0). Имеется также одна веха (Модис – Курцвейл 26 = Панов 18), которую Модис и Панов датируют одинаково, но которой они дают различные названия.

3. Имеется несколько вех, которым Модис и Панов дают отдаленно сходные названия и примерно (но не в точности) сходные датировки (например, Модис – Курцвейл 23 ≈ Панов 16; Модис – Курцвейл 19 ≈ Панов 12; Модис – Курцвейл 17 ≈ Панов 11; Модис – Курцвейл 9 ≈ Панов 5). В одном случае Модис и Панов дают одной и той же вехе (Модис – Курцвейл 5 ~ Панов 2) одинаковое название, но очень разные даты.

4. С другой стороны, для очень значительных отрезков рассматриваемых рядов корреляция между ними выглядит крайне удаленной. Например, для периода между 400 млн. лет назад и 150 тыс. лет назад эта корреляция выглядит следующим образом (см. табл. 2). Как видим, для очень большой части планетарной истории (между Кембрийским взрывом и возникновением Homo sapiens sapiens) корреляция между двумя рядами выглядит реально слабой; вполне очевидно, что речь идет о совершенно независимо составленных (и достаточно отличных друг от друга) списках.

Таблица 2

Корреляция между списками фазовых переходов Модиса и Панова для периода между 400 млн. лет назад и 150 тыс. лет назад

Ряд Модиса – Курцвейла

Ряд Панова (2005)

6. Первые млекопитающие, первые птицы, первые динозавры – 210 млн. лет назад. 7. Первые покрытосеменные, древнейшие остатки цветковых растений – 139 млн. лет назад. 8. Первые приматы / столкновение с астероидом / массовое вымирание (включая динозавров) – 54,6 млн. лет назад. 9. Первые человекообразные обезьяны, первые гоминиды – 28,5 млн. лет назад. 10. Первый орангутан, проконсул – 16,5 млн. лет назад. 11. Расхождение предков шимпанзе и человека, самые ранние свидетельства прямохождения у гоми- нид – 5,1 млн. лет назад. 12. Первые каменные орудия, Homo erectus – 2,2 млн. лет назад. 13. Возникновение Homo sapiens – 555 тыс. лет назад. 14. Освоение огня / Homo heidelbergensis – 325 тыс. лет назад. 15. Расхождение типов человеческой ДНК – 200 тыс. лет назад

3. Начало мезозойской эры, революция пресмыкающихся – 235 млн. лет назад. 4. Начало кайнозойской эры, революция млекопитающих – 66 млн. лет назад. 5. Начало неогена – 25–20 млн. лет назад. 6. Начало четвертичного периода (антропоген) – 4,4 млн. лет назад. 7. Олдувай, палеолитическая революция – 2,0–1,6 млн. лет назад. 8. Шелль – 600–700 тыс. лет назад. 9. Ашель – 400 тыс. лет назад

Временной ряд Панова: формальный анализ

Теперь, после того как мы уже знаем все это, проанализируем ряд Панова тем же самым способом, как мы проанализировали выше ряд Модиса – Курцвейла. Результаты этого анализа выглядят следующим образом (см. рис. 13):

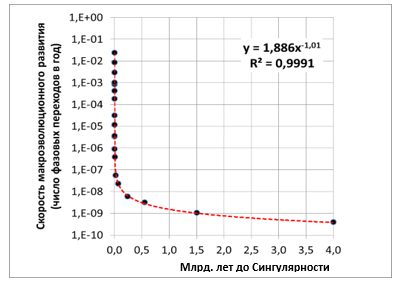
Рис. 13. Диаграмма рассеивания точек фазовых переходов Панова с наложенной линией степенной регрессии
(с логарифмической шкалой по оси ординат) – для определенной методом наименьших квадратов
даты Сингулярности = 2027 год н. э.

В двойной логарифмической шкале соответствие между степенной моделью y = 1,886 / x^1,01 (где x обозначается число лет до точки Сингулярности, определенной методом наименьших квадратов как 2027 год н. э.) и эмпирическими оценками Панова выглядит следующим образом (см. рис. 14):

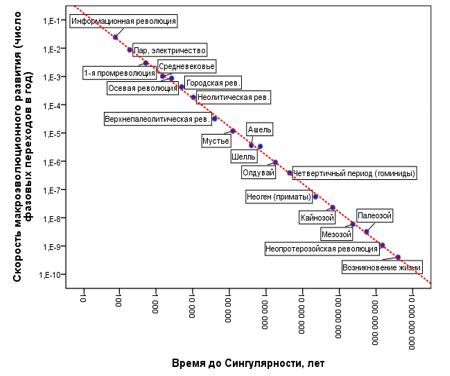
Рис. 14. Диаграмма рассеивания точек фазовых переходов Панова с наложенной линией степенной регрессии
(в двойной логарифмической шкале) – для определенной методом наименьших квадратов даты Сингулярности = 2027 год н. э.

Я, конечно, ожидал, что уравнение, лучше всего описывающее ряд Панова, будет выглядеть достаточно похожим на уравнение, которое мы выше получили для ряда Модиса – Курцвейла; но, честно скажу, я не ожидал, что оно окажется до такой степени похожим. Это особенно впечатляет, если принимать во внимание то обстоятельство, что ни Модис, ни Панов не предпринимали попыток аппроксимировать свои ряды при помощи уравнения (10), а потому их никак нельзя подозревать в попытках «подогнать» свои ряды под это уравнение. Действительно, в неупрощенном виде степенное уравнение, лучше всего описывающее прослеживаемый в ряду Модиса – Курцвейла паттерн ускорения планетарного макроэволюционного развития, выглядит следующим образом:

(8)

где, напомним, y – это скорость макроэволюционного развития (измеряемая как число фазовых переходов за единицу времени), а 2029 (год н. э.) – точка Сингулярности, определенная методом наименьших квадратов. В то же время степенное уравнение, лучше всего описывающее паттерн ускорения планетарного макроэволюционного развития, прослеживаемый в ряду Панова (2005), выглядит следующим образом:

Вот как выглядит соответствующее уравнение в общем виде:

Это уравнение имеет три параметра – C, t* и β. И, как мы видели, все три параметра оказались удивительно близкими, как для ряда Курцвейла – Модиса, так и для ряда Панова.

Формулы ускорения глобального макроэволюционного развития в рядах Модиса – Курцвейла и Панова: сравнительный анализ

Действительно, сравнение уравнений типа (10), наиболее точно математически описывающих два соответствующих ряда, дает следующие результаты (см. табл. 3):

Собственно говоря, на меня наиболее сильное впечатление произвело даже не то обстоятельство, что значение параметра Сингулярности (t*) для обеих регрессий оказалось столь близким (разница всего в два года!), а то, что значение показателя степени β в обоих случаях оказалось столь близким к 1.

Особого упоминания заслуживает исключительно высокая корреляция между теоретическими кривыми, генерируемыми чрезвычайно простыми уравнениями типа (5), и эмпирическими оценками как Модиса – Курцвейла, так и Панова. Применительно к ряду Модиса – Курцвейла уравнение (5) описывает 99,89 % всей вариации скорости глобальной эволюции на протяжении нескольких миллиардов лет, в то время как для ряда Панова это соответствие составляет 99,91 % – вместе с тем предельная близость значений R² для обеих регрессий (разница между ними составляет всего лишь 0,02 %!) впечатляет и сама по себе [11].

И, конечно же, не вызывает никакого удивления то, что дифференциальное уравнение, описывающее ускорение темпов роста глобальной сложности в ряду Панова, оказывается крайне сходным с формулой ускорения темпов глобального макроэволюционного развития для ряда Модиса – Курцвейла. Действительно, как мы уже упоминали, имеются достаточные основания упростить уравнение (9) до простого гиперболического варианта (11):

Напомним, такое алгебраическое уравнение может рассматриваться как решение следующего дифференциального уравнения, которое оказывается крайне сходным с тем, что мы выше получили для ряда Модиса – Курцвейла:

Таким образом, общая формула ускорения темпов глобального макроэволюционного развития, столь точно описывающая пановскую серию «биосферных революций», оказывается практически идентичной той, что была нами обнаружена для ряда Модиса – Курцвейла: увеличение темпов макроэволюционного развития в a раз сопровождается увеличением скорости роста (т. е. ускорения) темпов макроэволюционного развития в a² раз; так, двукратное увеличение темпов макроэволюции в тенденции сопровождается четырехкратным увеличением скорости роста (т. е. ускорения) темпов макроэволюции; десятикратное увеличение темпов макроэволюционного развития в тенденции сопровождается стократным ускорением роста темпов макроэволюционного развития и т. д. На мой взгляд, все это говорит о наличии достаточно строгих глобальных макроэволюционных закономерностей (описывающих рост сложности на нашей планете на протяжении нескольких миллиардов лет), которые могут удивительно точно описываться крайне простыми математическими функциями.

Удивительное открытие Хайнца фон Ферстера

Здесь уместно вспомнить о том, что в 1960 году Х. фон Ферстер, П. Мора и Л. Амиот опубликовали в журнале Science сообщение об удивительном открытии (von Foerster et al. 1960). Они показали, что между 1 и 1958 годами н. э. динамика численности народонаселения мира (N) может быть с необычайно высокой точностью описана при помощи следующего поразительно простого уравнения:

где N_t – это население мира в момент времени t, a C и t* – константы, при этом t* соответствует так называемой демографической сингулярности. Параметр t* был оценен фон Ферстером и его коллегами как 2026,87, что соответствует 13 ноября 2026 года; это, кстати, предоставило им возможность дать своей статье предельно броское название «Конец света: пятница, 13 ноября 2026 года от Рождества Христова» (Ibid.); однако позже было показано, что эта тенденция просматривалась какое-то время и после 1958 года (см., например: Капица 1999; Коротаев и др. 2010), а с другой стороны, эта же тенденция прослеживается и в течение многих тысячелетий до н. э. (Капица 1996; 1999; Подлазов 2000; 2001; 2002; Коротаев 2006; 2010а; Коротаев, Малков, Халтурина 2005а; 2007; Kapitza 1996; 2003; Kremer 1993; Tsirel 2004; Korotayev, Malkov, Khaltourina 2006a; 2006b). Более того, М. Кремер (Kremer 1993) утверждает, что эта тенденция прослеживается с 1 000 000 лет назад, а С. П. Капица (1996; 1999) даже настаивал на том, что ее можно проследить начиная примерно с 4 000 000 года до н. э.

Трудно не заметить, что паттерн ускорения темпов роста численности населения мира, обнаруженный еще в 1960 году фон Ферстером в эмпирических данных по динамике численности населения Земли между 1 и 1958 годами н. э., оказывается практически идентичным тому паттерну ускорения темпов глобального развития, который мы выше обнаружили во временных рядах как Модиса – Курцвейла, так и Панова. Особо отметим, что степенная регрессия для всех трех рядов дала значение показателя степени β, крайне близкое к 1 (1,003 для ряда Модиса – Курцвейла, 1,01 для ряда Панова и 0,99 у Х. фон Ферстера для динамики численности населения мира).

Однако и обнаруженная крайняя близость значений параметра t* (а это именно значение точки Сингулярности) также не может не впечатлить: степенная регрессия дает в качестве точки Сингулярности 2029 год для ряда Модиса – Курцвейла, 2027 год – для ряда Панова и в точности тот же 2027 год для ряда фон Ферстера.

Мы уже говорили выше, что, как и в случае с уравнениями (8) и (9), в уравнении фон Ферстера (13) значение степени в знаменателе (0,99) столь слабо отлично от 1, что, как уже предлагалось
С. фон Хернером (von Hoerner 1975) и С. П. Капицей (1992; 1999), его целесообразно использовать в следующем упрощенном виде:

Полученное в результате этого уравнение полностью идентично вышеприведенному уравнению (5), которое оказалось способным описать с чрезвычайно высокой точностью общий паттерн ускорения темпов глобального развития в течение как минимум последних 4 млрд. лет. Отметим, что уравнение (14) оказалось способным описать тренд динамики численности населения мира (вплоть до начала 1970-х годов) с такой же предельно высокой точностью, с какой уравнение (5) способно описать ускорение темпов роста глобальной сложности (как минимум за последние 4 млрд. лет). Ниже имеет смысл продемонстрировать это для уравнения фон Ферстера (14).

Действительно, заменим в уравнении (14) t* на 2027 (это просто результат округления полученного фон Ферстером значения точки Сингулярности, 2026,87), а C – на 215 000 [12]. Это даст нам вариант уравнения фон Ферстера – фон Хернера – Капицы с определенными параметрами:

Общее совпадение кривой, описываемой уравнением фон Ферстера, и наиболее детального ряда эмпирических оценок выглядит следующим образом (см. рис. 15):

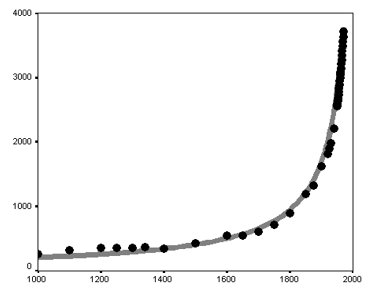
Рис. 15. Корреляция между эмпирическими оценками долгосрочной динамики численности населения мира (в млн. человек,
1000–1970 годы) и кривой, генерируемой уравнением фон Ферстера (15)

Примечание: черные маркеры соответствуют эмпирическим оценкам численности населения мира, сделанным Р. МакЭведи и К. Джонсом (McEvedy, Jones 1978) для 1000–1950 гг., и эмпирическим оценкам Отдела народонаселения ООН (UN Population Division 2018) для периода с 1950 по 1970 год. Серая кривая сгенерирована уравнением фон Ферстера (15). Формальные характеристики этой корреляции таковы: r = 0,998; R² = 0,996; p = 9,4 × 10^-17 ≈ 1 × 10^-16.

Таким образом, на самом деле уравнение (14) оказывается способным описать динамику ускорения роста численности населения мира (вплоть до начала 1970-х годов) таким же удивительно точным образом, каким уравнение (5) способно описать общий паттерн глобального макроэволюционного ускорения за последние 4 млрд. лет.

В контексте Большой истории очень важным представляется то обстоятельство, что уравнение (5), описывающее ускорение темпов глобального макроэволюционного ускорения, и уравнение (14), описывающее рост численности населения Земли, оказываются полностью идентичными. Более того, эмпирический и математический анализ показывает, что между ними существует очень глубокая взаимосвязь и что они описывают две стороны одного процесса (см.: Korotayev 2018: 106–110).

О формуле ускорения глобальной эволюции

Честно скажу, у меня были серьезные сомнения, когда я впервые ознакомился с расчетами А. Д. Панова и Т. Модиса (и я не удивлен, что у большинства историков возникают очень похожие сомнения, когда они видят эти работы). У меня появилось много возражений относительно точности многих описаний их «канонических вех», адекватности их отбора и точности датировок. Я начал серьезно относиться к расчетам Модиса и Панова, только когда сам проанализировал два соответствующих временных ряда, идентифицированных (как мы видели выше) полностью независимо друг от друга двумя разными исследователями, использующими совершенно разные источники. При этом я анализировал их при помощи математической модели, которая не применялась ни Модисом, ни Пановым, и обнаружил, что они описываются необычайно точным образом почти идентичной математической гиперболической функцией. На мой взгляд, это заставляет предполагать объективное наличие довольно простой гиперболической закономерности ускорения глобального макроэволюционного развития, наблюдаемого на Земле в течение последних 4 млрд. лет. Это впечатление стало еще более сильным, когда уравнение, описывающее картину ускорения планетарной макроэволюции в рядах Модиса – Курцвейла и Панова, оказалось полностью идентичным уравнению, найденному еще в 1960 году фон Ферстером, показавшим уже тогда, что оно способно с необычайной точностью описать глобальный паттерн ускорения роста численности населения Земли между 1 и 1958 годами.

У меня были основания ожидать, что планетарное макроэволюционное ускорение за последние 4 млрд. лет может быть описано единым гиперболическим уравнением с достаточно высокой точностью, так как предыдущие исследования показали, что и биологическая, и социальная эволюция может описываться с достаточно высокой точностью простыми гиперболическими уравнениями [13], но, должен сказать, и я был удивлен, когда обнаружил, что ускорение за последние 4 млрд. лет описывается единым гиперболическим уравнением с такой высокой точностью.

Также небезынтересным представляется то обстоятельство, что даты сингулярности для всех трех (очень различных) рассмотренных нами временных рядов оказались практически идентичными (2029 год для ряда Модиса – Курцвейла и 2027 год – для рядов Панова и фон Ферстера).

К интерпретации Сингулярности. Место Сингулярности в Большой истории и глобальной эволюции

Но насколько серьезно мы должны относиться к «предсказанию» Сингулярности, содержащемуся в таких математических моделях? Следует ли нам вместе с Р. Курцвейлом действительно ожидать, что где-то в районе 2029 года мы будем иметь дело с ускорением глобального технологического роста на несколько порядков (что действительно вытекает из уравнения (4), если понимать его буквально, как предлагает, например, А. П. Назаретян [2015a; 2015б; Nazaretyan 2015; 2016; 2017; 2018])? Например, можем ли мы использовать то обстоятельство, что наш анализ ряда Модиса – Курцвейла выявил Сингулярность в районе 2029 года как указание на то, что в районе этого времени нам следует ожидать начало девятой пороговой вехи Большой истории?

Отметим, что некоторые специалисты в области Большой истории склонны относиться к таким «математически обоснованным» предсказаниям совершенно серьезно. Например, А. П. Назаретян в статье с симптоматическим заголовком «Мегаистория и ее “загадочная сингулярность”» утверждает следующее: «Солнечная система образовалась около 4,6 млрд. лет назад, а самые первые признаки жизни на Земле насчитывают до 4 млрд. лет. Таким образом, наша планета стала одной из (вероятно, множества) точек, на которых локализовалась последующая эволюция Метагалактики. Хотя ее ускорение замечено давно, в последнее время обнаружилось новое обстоятельство. Австралийский экономист и историк-глобалист Г. Снукс, российский физик А. Д. Панов и американский математик Р. Курцвейл независимо, по разным источникам и с использованием разного математического аппарата сопоставили временные интервалы между глобальными фазовыми переходами в биологической, прасоциальной и социальной эволюции (Панов 2005; 2008; Kurzweil 2005; Snooks 1996; Вайнберг 1981). Расчеты показывают, что периоды сокращались по строго убывающей геометрической прогрессии, то есть ускорение эволюции на Земле следовало логарифмическому закону» (Назаретян 2015a: 759). И далее: «Экстраполировав линию гиперболического ускорения в будущее, исследователи пришли к единодушному и еще более шокирующему выводу: около середины XXI века она упирается в точку финальной (большой) сингулярности. Кривая заворачивает в вертикаль, то есть скорость эволюционного процесса стремится к бесконечности, а интервалы между фазовыми переходами – к нулю» (Там же: 761; см. также: Nazaretyan 2017: 32).

Назаретян использует математические расчеты даты Сингулярности глобальной эволюционной гиперболы для предсказания возможной даты того, что в терминологии основоположника Большой истории Д. Кристиана (Christian 2008) можно было бы назвать девятой пороговой вехой Большой истории (Big History Threshold 9), которая, согласно Назаретяну, будет существенно более значимой, чем предшествующие вехи 7 («Аграрная революция») и 8 («Модернизационная революция») [14].

Однако дают ли расчеты, проведенные Пановым в 2003–2005 годах или нами в этой статье, действительные основания ожидать Сингулярности / наступления девятой пороговой вехи Большой истории между 2029 и 2050 годами? Как, наверное, уже понятно, я склонен дать на этот вопрос однозначно отрицательный ответ. Собственно говоря, как мы могли видеть, данная статья представляет собой, судя по всему, первую попытку в явном виде (говоря словами А. П. Назаретяна [2015а: 761]) «экстраполировать линию гиперболического ускорения в будущее» [15]. Хотя Назаретян и утверждает обратное, подобная попытка не предпринималась Г. Д. Снуксом (Snooks 1996), который не пытался вычислять какие бы то ни было математические сингулярности. Никаких формальных попыток «экстраполировать линию гиперболического ускорения в будущее» с использованием каких-либо математических методов Курцвейлом не предпринималось – уже хотя бы потому, что он до сих пор уверен в том, что имеет дело с экспоненциальным, а не гиперболическим ускорением. Таким образом, едва ли не единственным исследователем, попытавшимся математически рассчитать время сингулярности для линии ускорения планетарной эволюции, был А. Д. Панов (2004; 2005; 2006; 2008; Panov 2005; 2011; 2017) – хотя с некоторыми оговорками здесь можно также упомянуть С. Н. Гринченко (2001; 2004; 2006; 2007 и др.), Т. Модиса (Modis 2002; 2003) и Д. ЛеПуара (LePoire 2013; 2015).

Использованная Пановым методика расчета Сингулярности существенно отличалась от «экстраполирования линии гиперболического ускорения в будущее» (это, скорее, та самая методика, которая была использована нами, а не Пановым); однако нет сомнений в том, что им была применена не менее строгая методика расчета времени Сингулярности планетарной эволюции. Но каковы были результаты этих расчетов? После того как А. Д. Панов применил свою методику математического анализа к временному ряду, начинающемуся с фазового перехода 0 («Возникновение жизни на Земле») и заканчивающемуся на фазовом переходе 19 («Кризис и распад социалистического лагеря, информационная глобализация»), он обнаружил, что точка сингулярности для его временного ряда находится вовсе не «около середины XXI века», как это утверждает А. П. Назаретян (2015а: 761), а приходится на 2004 год н. э. (!) [16] (Панов 2005: 130; Panov 2005: 222). При этом Назаретян, кажется, даже не заметил, что вскоре после обнаружения точки Сингулярности Панов занялся изучением постсингулярного развития человечества (и вообще вопросом о постсингулярных цивилизациях) и тесно связанным с этим вопросом о глобальном замедлении темпов научно-технического прогресса (Панов 2009; 2013; Panov 2011; 2017).

Как пишет Д. ЛеПуар, «прослеживаемые в Большой истории тенденции к ускоряющимся изменениям и росту сложности и связанная с ними тенденция к ускоренному росту потребления энергии не могут продолжаться до бесконечности. Мы исследовали признаки потенциального замедления темпов изменений в экономике, технологии и социальной сфере. Это не означает, что изменения прекратятся, просто темпы изменений уже не будут ускоряться. Фактически к точке перегиба в логистической кривой обучения была сделана только половина открытий. Поскольку в истории жизни, человека и технологической цивилизации было три основных этапа, продолжение логистической кривой предполагает еще три фазы. Направление развития технологий указывает на следующий этап, включая усовершенствованные технологии изменения природы человека посредством усовершенствованных биотехнологий и компьютерной интеграции… Слишком быстрое изменение не всегда хорошо. Оно приводит к тому, что эффективность систем падает, потому что мы имеем мало долгосрочных ожиданий» (LePoire 2013: 115–116). В качестве важных факторов начавшегося замедления темпов глобального развития ЛеПуар называет «рост себестоимости производимой энергии, ограниченные природные ресурсы, снижение темпов фундаментальных открытий в области физических наук и необходимость инвестиций в охрану окружающей среды» (Ibid.: 109).

Отметим также, что Т. Модис (Modis 2002; 2003; 2005; 2012) тоже интерпретирует максимальное ускорение темпов роста глобальной сложности, выявляемое им в районе 2000 года н. э., именно как точку перегиба, после которой он прогнозирует последовательное снижение темпов роста глобальной сложности. Еще раньше попытка математически выявить Сингулярность в ряду событий планетарной эволюции [17], которые Модис назвал бы «каноническими вехами», была предпринята в 2001 году (т. е. всего за год до публикации его основополагающей статьи) С. Н. Гринченко (2001; см. также: Гринченко 2004; 2006; 2007; 2015; Гринченко, Щапова 2017); точка Сингулярности была им математически определена как 1981 год н. э. Отметим, что это хорошо коррелирует с идентификацией нами 1973 года как точки перегиба; после квадратично-гиперболический тренд ускорения роста мирового ВВП начал меняться на прямо противоположный тренд к замедлению роста этого показателя (Коротаев 2006; Коротаев, Малков, Халтурина 2007; Коротаев и др. 2010; Коротаев, Божевольнов 2010; Акаев и др. 2014; Садовничий и др. 2014; Коротаев, Билюга 2016; Khaltourina, Korotayev 2007). Все это хорошо подтверждается растущим объемом данных, свидетельствующих о начале долгосрочной тенденции к замедлению темпов научно-технического и экономического роста (см., например: Крылов 1999; 2002; 2007; Панов 2009; 2013; Акаев 2010; Коротаев, Малков, Халтурина 2007; Коротаев, Божевольнов 2010; Коротаев и др. 2010; Коротаев, Билюга 2016; Huebner 2005; Khaltourina, Korotayev 2007; Maddison 2007; Modis 2002; 2005; 2012; Gordon 2012; Teulings, Baldwin 2014; Piketty 2014; LePoire 2005; 2009; 2013; 2015; 2016; Summers 2016; Cervellati et al. 2017; Taylor, Tyers 2017; Jones 2018; Popović 2018 etc.).

Итак, насколько серьезно мы должны относиться к «предсказанию» сингулярности, содержащемуся в гиперболических математических моделях глобального развития? Или – следует ли нам вместе с Курцвейлом ожидать, что где-то в районе 2029 года мы будем реально иметь дело с ускорением глобального технологического роста на несколько порядков (что действительно вытекает из уравнения (4), если понимать его буквально)?

Как уже понятно, я склонен дать на этот вопрос однозначно отрицательный ответ. И в заключение приведу еще один аргумент. На мой взгляд, отрицательный ответ на этот вопрос вытекает, например, из известных нам эмпирических данных по динамике численности населения мира и установленных к настоящему времени механизмов этой динамики. Как мы помним, формула гиперболического роста численности населения Земли, открытая Х. фон Ферстером, идентична формуле ускорения темпов глобального развития, прослеживаемого в рядах Модиса – Курцвейла и Панова, и она характеризуется параметром сингулярности (2027 год н. э.), который просто идентичен для формулы ускорения в ряду Панова и имеет разницу всего лишь в 2 года для ряда Модиса – Курцвейла. Однако каковы основания ожидать, что к пятнице 13 ноября 2026 года темпы прироста населения мира увеличатся на несколько порядков, как это подразумевает уравнение фон Ферстера? Ответ на вопрос ясен: нет никаких оснований этого ожидать. Несомненно, когда фон Ферстер и его коллеги давали своей статье (von Foerster et al. 1960) знаменитое название «Судный день: пятница, 13 ноября 2026 года», они вовсе не имели в виду, что население Земли в этот день действительно может стать бесконечным (хотя «эсхатологические» выводы из гиперболических моделей роста Мир-Системы без каких-либо достаточных на то оснований делаются до сих пор [см., например: Johansen, Sornette 2001]). Из этой статьи, скорее, вытекал прямо противоположный прогноз – наблюдавшийся вплоть до 1960 года на протяжении многих веков гиперболический рост мирового населения должен испытать в самые ближайшие годы радикальную трансформацию и смениться принципиально иным типом демографической макродинамики. Отметим, что этот прогноз стал блестяще оправдываться всего лишь через несколько лет после публикации статьи фон Ферстера и его коллег (Коротаев, Малков, Халтурина 2007). Мир-Система начала выходить из режима с обострением (Они же 2008: 99; см. также: Коротаев, Халтурина 2009; Зинькина и др. 2016; Зинькина, Коротаев 2017; Korotayev 2008: 154).

Действительно, с начала 1970-х годов кривая роста численности населения мира стала все больше отклоняться от гиперболической траектории (см., например: Капица 1999; Коротаев, Малков, Халтурина 2005а; 2007; Коротаев 2015; 2016; Kapitza 2003; 2006; 2010; Livi-Bacci 2012; Korotayev, Malkov, Khaltourina 2006a; 2006b; Korotayev, Goldstone, Zinkina 2015; Grinin, Korotayev 2015), и за последние десятилетия она приняла определенно логистическую форму – тенденция к гиперболическому ускорению сменилась тенденцией к логистическому замедлению.

В некоторых отношениях вполне можно сказать, что фон Ферстер открыл сингулярность глобальной демографической истории; он обнаружил, что человеческая Мир-Система приближалась к сингулярному периоду в своей истории, когда тенденция гиперболического ускорения, которой она следовала много тысячелетий (а по мнению некоторых, даже несколько миллионов лет), будет заменена на противоположный тренд к замедлению. Именно через этот сингулярный период мы сейчас и проходим. Процессы и механизмы данного разворота трендов к настоящему времени очень тщательно изучены и известны как «глобальный демографический переход» (Капица 1999; 2007; Подлазов 2001; 2017; Романчук, Медведева 2009; Коротаев 2015; Kapitza 2003; 2006; 2010; Korotayev, Goldstone, Zinkina 2015; Podlazov 2017). При этом особое внимание здесь стоит обратить на то обстоятельство, что в случае с глобальной демографической эволюцией переход от гиперболического ускорения к логистическому замедлению начался за несколько десятилетий до даты Сингулярности, математически вычисленной фон Ферстером.

На мой взгляд, имеются основания утверждать, что замедление скорости глобального макроэволюционного развития уже началось  – и началось оно также за несколько десятилетий до той точки Сингулярности, которую можно математически выявить в глобальных эволюционных рядах Модиса – Курцвейла и Панова.

Заключение

Итак, проведенный нами анализ позволяет предполагать наличие достаточно строгих макроэволюционных закономерностей (описывающих эволюцию сложности на нашей планете за последние несколько миллиардов лет), которые могут удивительно точно описываться крайне простыми математическими функциями. Вместе с тем этот анализ заставляет предполагать, что в районе точки Сингулярности нет основания вслед за Курцвейлом ожидать невиданного (на много порядков) ускорения темпов технологического развития; имеются бóльшие основания интерпретировать эту точку как индикатор зоны перегиба, после прохождения которой темпы глобальной эволюции будут систематически в долгосрочной перспективе замедляться.

Литература

Акаев, А. А. 2010. Фундаментальные пределы экономического роста и потребления. В: Халтурина, Д. А., Коротаев, А. В., Зинькина, Ю. В. (ред.), Системный мониторинг глобальных и региональных рисков. М.: URSS, с. 12–30.

Акаев, A. А., Коротаев, А. В., Малков, С. Ю. 2014. Современная ситуация и контуры будущего. В: Коротаев, А. В., Малков, С. Ю., Акаев, А. А. (отв. ред.), Комплексный системный анализ, математическое моделирование и прогнозирование развития стран БРИКС. Предварительные результаты. М.: Красанд/URSS, с. 10–31.

Антисери, Д., Реале, Дж. 2001. Западная философия от истоков до наших дней. Античность, Средневековье. СПб.: Петрополис.

Балашова, Н. А., Савченко, В. А., Сажиенко, Е. В., Назаретян, А. П. 2017. Мегаистория и глобальные вызовы XXI века: синергетическая модель. Историческая психология и социология истории 10(1): 193–212.

Биган, Д. 2004. Планета человекообразных. В мире науки 11: 68–77.

Борисковский, П. И.

   1970. Ашельская культура. В: Прохоров, А. М. (гл. ред.), Большая советская энциклопедия. Т. 2. М.: Советская энциклопедия, с. 471.

   1974a. Олдовай. В: Прохоров, А. М. (гл. ред.), Большая советская энциклопедия. Т. 18. М.: Советская энциклопедия, с. 369.

   1974б. Мустьерская культура. В: Прохоров, А. М. (гл. ред.), Большая советская энциклопедия. Т. 17. М.: Советская энциклопедия, с. 134.

   1978. Шелльская культура. В: Прохоров, А. М. (гл. ред.), Большая советская энциклопедия. Т. 29. М.: Советская энциклопедия, с. 377.

Вайнберг, С. 1981. Первые три минуты. Современный взгляд на происхождение Вселенной. М.: Энергоиздат.

Вонг, К. 2003. У колыбели Homo sapiens. В мире науки 11: 9–10.

Галимов, Э. М. 2001. Феномен жизни: между равновесием и нелинейностью. Происхождение и принципы эволюции. М.: URSS.

Гринченко, С. Н.

   2001. Социальная метаэволюция Человечества как последовательность шагов формирования механизмов его системной памяти. Электронный журнал «Исследовано в России» 145: 1652–1681.

   2004. Системная память живого (как основа его метаэволюции и периодической структуры). М.: Мир.

   2006. История Человечества с информатико-кибернетических позиций: проблемы периодизации. В: Гринин, Л. Е., Коротаев, А. В., Малков, С. Ю., (отв. ред.), История и Математика: Проблемы периодизации исторических макропроцессов. М.: КомКнига, с. 38–52.

   2007. Метаэволюция (систем неживой, живой и социально-технологической природы). М.: ИПИ РАН.

   2015. Моделирование: индуктивное и дедуктивное. Проблемы исторического познания. М.: ИВИ РАН, с. 95–101.

Гринченко, С. Н., Щапова, Ю. Л. 2017. Палеоантропология, хронология и периодизация археологической эпохи: числовая модель. Пространство и Время 1(27): 72–82.

Дьяконов, И. М. 1994. Пути истории. От древнейшего человека до наших дней. М.: Вост. лит-ра.

Заварзин, Г. А. 2003. Становление системы биогеохимических циклов. Палеонтологический журнал 6: 16–24.

Зайцев, А. И. 2001. Из наследия А. И. Зайцева. Т. 1. Культурный переворот в Греции VIII–V вв. до н. э. СПб.: Петрополис.

Зинькина, Ю. В., Коротаев, А. В. 2017. Социально-демографическое развитие стран Тропической Африки: ключевые факторы риска, модифицируемые управляющие параметры, рекомендации. М.: Ленанд/URSS.

Зинькина, Ю. В., Шульгин, С. Г., Коротаев, А. В. 2016. Эволюция глобальных сетей. Закономерности, тенденции, модели. М.: Ленанд/URSS.

Капица, С. П.

   1992. Математическая модель роста населения мира. Математическое моделирование 4(6): 65–79.

   1996. Феноменологическая теория роста населения Земли. Успехи физических наук 166(1): 63–80.

   1999. Сколько людей жило, живет и будет жить на земле. М.: Наука.

   2007. Демографический переход и будущее человечества. Вестник Европы 21: 7–16.

Келлер, Б. М. 1975. Палеозойская группа (эра). В: Прохоров, А. М. (гл. ред.), Большая советская энциклопедия. Т. 19. М.: Советская энциклопедия, с. 103–104.

Коротаев, А. В.

   2006. Периодизация истории Мир-Системы и математические макромодели социально-исторических процессов. В: Гринин, Л. Е., Коротаев, А. В., Малков, С. Ю. (отв. ред.), История и Математика: Проблемы периодизации исторических макропроцессов. М.: URSS, с. 116–167.

   2007. Макродинамика урбанизации Мир-Системы: количественный анализ. В: Малков, С. Ю., Гринин, Л. Е., Коротаев, А. В. (ред.), История и Математика: Макроисторическая динамика общества и государства. М.: КомКнига/URSS, с. 21–39.

   2010а. Компактные математические модели долгосрочного развития Мир-Системы. Уральский исторический вестник 3: 15–24.

   2010б. Компактные математические модели развития Мир-Системы. В: Акаев, А. А.,  Коротаев, А. В., Малинецкий, Г. Г. (отв. ред.), Прогноз и моделирование кризисов и мировой динамики. М.: ЛКИ/URSS, с. 70–92.

   2015. Глобальный демографический переход и фазы дивергенции – конвергенции центра и периферии Мир-Системы. Вестник Института экономики Российской академии наук 1: 149–162.

   2016. Великая дивергенция и великая конвергенция как фазы процесса модернизации. География мирового развития: сб. науч. тр. Вып. 3. М.: Тов. научных изданий КМК, с. 49–60.

Коротаев, А. В., Билюга, С. Э. 2016. О некоторых современных тенденциях мирового экономического развития. Вестник Института экономики Российской академии наук 4: 20–39.

Коротаев, А. В., Божевольнов, Ю. В. 2010. Некоторые общие тенденции экономического развития Мир-Системы. В: Акаев, А. А., Коротаев, А. В., Малинецкий, Г. Г., Прогноз и моделирование кризисов и мировой динамики. М.: ЛКИ/URSS, с. 161–171.

Коротаев, А. В., Комарова, Н. Л., Халтурина, Д. А. 2007. Законы истории. Вековые циклы и тысячелетние тренды. Демография. Экономика. Войны. М.: КомКнига/URSS.

Коротаев, А. В., Малков, А. С., Халтурина, Д. А.

   2005а. Законы истории. Математическое моделирование исторических макропроцессов. Демография. Экономика. Войны. М.: КомКнига/ URSS.

   2005б. Компактная математическая макромодель технико-экономического и демографического развития Мир-Системы (1–1973 гг.). В: Коротаев, А. В., Малков, С. Ю. (ред.), История и синергетика: Математическое моделирование социальной динамики. М.: URSS/КомКнига, с. 6–48.

   2007. Законы истории: Математическое моделирование развития Мир-Системы. Демография, экономика, культура. М.: КомКнига/URSS.

   2008. Компактная математическая модель экономического и демографического развития Мир-Системы (1–1973 гг.). Экономика и математические методы 44(4): 90–101.

Коротаев, А. В., Марков, А. В. 2006. Механизм гиперболического роста в биологических и социальных системах. Философские науки 11: 138–141.

Коротаев, А. В., Халтурина, Д. А. 2009. Современные тенденции мирового развития. М.: ЛИБРОКОМ/URSS.

Коротаев, А. В., Халтурина, Д. А., Малков, А. С., Божевольнов, Ю. В., Кобзева, С. В., Зинькина, Ю. В. 2010. Законы истории. Математическое моделирование и прогнозирование мирового и регионального развития. 3-е изд., испр. и доп. М.: ЛКИ/URSS.

Кринг, Д., Дурда, Д. Д. 2004. День, когда мир был сожжен. В мире науки 3: 56–63.

Крылов, О. В.

   1999. Будет ли конец науки. Российский химический журнал 43(6): 96–106.

   2002. Динамика развития химической науки. Российский химический журнал 46(3): 96–99.

   2007. Современная наука: близкий конец или завершение очередного этапа? Российский химический журнал 51(3): 71–78.

Кэрролл, Р.

   1992. Палеонтология и эволюция позвоночных. Т. 1. М.: Мир.

   1993а. Палеонтология и эволюция позвоночных. Т. 2. М.: Мир.

   1993б. Палеонтология и эволюция позвоночных. Т. 3. М.: Мир.

Лопатин, Н. В. 1983. Древние биосферы и генезис горючих ископаемых. Палеонтология и эволюция биосферы. Труды XXV сессии Всесоюзного палеонтологического общества. Вып. 6. Л.: АН СССР, с. 63–67.

Марков, A. В., Анисимов, В. А., Коротаев, А. В.

   2010. Взаимосвязь размера генома и сложности организма в эволюционном ряду от прокариот к млекопитающим. Палеонтологический журнал 4: 3–14.

   2011. Гиперэкспоненциальный рост минимального размера генома в эволюционном ряду от прокариот к млекопитающим. В: Гринин, Л. Е., Ильин, И. В., Коротаев, А. В., Марков, А. В. (ред.), Эволюция: дискуссионные аспекты глобальных эволюционных процессов. М.: ЛКИ, с. 113–154.

Марков, А. В., Коротаев, А. В.

   2007. Динамика разнообразия фанерозойских морских животных соответствует модели гиперболического роста. Журнал общей биологии 68(1): 3–18.

   2008а. Гиперболический рост разнообразия морской и континентальной биот фанерозоя и эволюция сообществ. Журнал общей биологии 69(3): 175–194.

   2008б. Гиперболический рост биоразнообразия в фанерозое объясняется ростом сложности и устойчивости сообществ. Современные проблемы биологической эволюции: материалы III Международной конференции к 130-летию со дня рождения Н. И. Вавилова и 110-летию со дня основания Государственного Дарвиновского музея. М.: Изд-во Государственного Дарвиновского музея, с. 278–323.

   2008в. Динамика разнообразия морской и континентальной биоты фанерозоя соответствует модели гиперболического роста. Геобиосферные события и история органического мира: тезисы докладов LIV сессии Палеонтологического общества при РАН (7–11 апреля 2008 г., Санкт-Пе-
тербург). СПб.: Палеонтологическое общество РАН, с. 108−110.

   2009а. Гиперболический рост в живой природе и обществе. М.: ЛИБРОКОМ/URSS.

   2009б. О причинах ускорения роста разнообразия морской и континентальной биоты фанерозоя: факты и модели. Синтетическая теория эволюции: состояние, проблемы, перспективы: программа и тезисы докладов Международной научной конференции, посвященной 200-летию со дня рождения Чарлза Дарвина и 150-летию выхода книги «Происхождение видов путем естественного отбора или сохранение благоприятствуемых пород в борьбе за жизнь». Луганск: Элтон-2, с. 37–39.

Муратов, М. В., Вахрамеев, В. А. 1974. Мезозойская группа (эра). В: Прохоров, А. М. (гл. ред.), Большая советская энциклопедия. Т. 16. М.: Советская энциклопедия, с. 6–8.

Назаретян, А. П.

   2004. Цивилизационные кризисы в контексте Универсальной истории. 2-е изд., перераб. и доп. М.: Пер се.

   2005. Знает ли история сослагательное наклонение? (Мегаисторический взгляд на альтернативные модели). Философские науки 2: 7–18.

   2009. Смыслообразование как глобальная проблема современности: синергетический взгляд. Вопросы философии 5: 3–19.

   2013. Середина XXI века: загадка сингулярности. Философские науки 9: 15–24.

   2014. «Национальная идея»: Россия в глобальных сценариях XXI века. Историческая психология и социология истории 7(1): 75–91.

   2015а. Мегаистория и ее «загадочная сингулярность». Вестник Российской академии наук 85(8): 755–764.

   2015б. Нелинейное будущее. Мегаистория, синергетика, культурная антропология и психология в глобальном прогнозировании. М.: Аргамак-Медиа.

Панов, А. Д.

   2004. Автомодельный аттрактор социально-биологической эволюции на Земле и гипотеза самосогласованного галактического происхождения жизни. Бюллетень Научно-культурного центра SETI Академии космонавтики им. К. Э. Циолковского 7(24): 4–21.

   2005. Сингулярная точка истории. Общественные науки и современность 1: 122–137.

   2006. Сингулярность Дьяконова. В: Гринин, Л. Е., Коротаев, А. В., Малков, С. Ю. (отв. ред.), История и Математика: Проблемы периодизации исторических макропроцессов. М.: КомКнига, с. 31–37.

   2008. Универсальная эволюция и проблема поиска внеземного разума (SETI). М.: ЛКИ/URSS.

   2009. Наука как явление эволюции. В: Гринин, Л. Е., Марков, А. В., Коротаев, А. В. (ред.), Эволюция: космическая, биологическая, социальная. М.: ЛИБРОКОМ, с. 99–127.

   2013. Макроэволюция и наука. Науковедческие исследования. М.: РАН, Ин-т информации по общественным наукам, с. 215–256.

Подлазов, А. В.

  2000. Теоретическая демография как основа математической истории. М.: ИПМ РАН.

  2001. Основное уравнение теоретической демографии и модель глобального демографического перехода. М.: ИПМ РАН.

  2002. Теоретическая демография. Модели роста народонаселения и глобального демографического перехода. В: Малинецкий, Г. Г., Курдюмов, С. П., Новое в синергетике. Взгляд в третье тысячелетие. М.: Наука, с. 324–345.

  2017. Теория глобального демографического процесса. Вестник Российской академии наук 6: 520–531.

Розанов, А. Ю.

  1986. Что произошло 600 миллионов лет назад. М.: Наука.

  2003. Ископаемые бактерии, седиментогенез и ранние стадии эволюции биосферы. Палеонтологический журнал 6: 41–49.

Розанов, А. Ю., Заварзин, Г. А. 1997. Бактериальная палеонтология. Вестник РАН 67(3): 241–245.

Романчук, А. А., Медведева, О. В. 2009. Глобальный демографический переход и его биологические параллели. В: Гринин, Л. Е., Марков, А. В., Коротаев, А. В. (ред.), Эволюция: космическая, биологическая, социальная. М.: ЛИБРОКОМ, с. 244–269.

Садовничий, В. А., Акаев, А. А., Коротаев, А. В., Малков, С. Ю. 2014. Комплексное моделирование и прогнозирование развития стран БРИКС в контексте мировой динамики. М.: Наука.

Федонкин, М. А. 2003. Сужение геохимического базиса жизни и эвкариотизация биосферы: причинная связь. Палеонтологический журнал 6: 33–37.

Фоули, Р. 1990. Еще один неповторимый вид. Экологические аспекты эволюции человека. М.: Мир.

Цирель, С. В. 2018. Big History и Singularity как метафоры, гипотезы и прогноз (рукопись статьи).

Шанцер, Е. В. 1973. Кайнозойская группа (эра). В: Прохоров, А. М. (гл. ред.), Большая советская энциклопедия. Т. 11. М.: Советская энциклопедия.

Ясперс, К. 1991. Смысл и назначение истории. М.: Политиздат.

A. H. 1975. Mesozoic era. In The New Encyclopedia Britannica. 15^th ed. Vol. 11. Chicago: Encyclopedia Britannica, Inc., pp. 1013–1017.

A. P. 1975. Cenozoic era. In The New Encyclopedia Britannica. 15^th ed. Vol. 3. Chicago: Encyclopedia Britannica, pp. 1079–1083.

Adams, H. 1969 [1909]. The Rule of Phase Applied to History. In Adams, H., The Degradation of the Democratic Dogma. New York, NY: Harper & Row, pp. 267–311.

Alvarez, L. W., Alvarez, W., Asaro, F., Michel, H. V. 1980. Extraterrestrial Cause for the Cretaceous-Tertiary Extinction. Science 208(4448): 1095–1108.

Barrow, J. D., Silk, J. 1980. The Structure of the Early Universe. Scientific American 242(4): 118–128.

Begun, D. R. 2003. Planet of the Apes. Scientific American 289(2): 64–73.

Burenhult, G. (ed.) 1993. The First Humans: Human Origins and History to 10,000 BC. San Francisco: Harper.

Callaghan, V., Miller, J., Yampolskiy, R., Armstrong, S. 2017. Technological Singularity. Dordrecht: Springer.

Carroll, R. L. 1988. Vertebrate Paleontology and Evolution. New York: W. H. Freeman and Co.

Cervellati, M., Sunde, U., Zimmermann, K. F. 2017. Demographic Dynamics and Long-run Development: Insights for the Secular Stagnation Debate. Journal of Population Economics 30(2): 401–432.

Christian, D. 2008. Big History: The Big Bang, Life on Earth, and the Rise of Humanity. Chantilly, VA: The Teaching Company.

Eden, A. H., Moor, J. H., Søraker, J. H., Steinhart, E. (eds.) 2012. Singularity Hypotheses: A Scientific and Philosophical Assessment. Berlin: Springer.

Foerster, H. von, Mora, P. M., Amiot, L. W. 1960. Doomsday: Friday, 13 November, AD 2026. Science 132(3436): 1291–1295.

Gordon, R. J. 2012. Is US Economic Growth Over? Faltering Innovation Confronts the Six Headwinds. Cambridge, MA: National Bureau of Economic Research.

Grinin, L., Korotayev, A. 2015. Great Divergence and Great Convergence. A Global Perspective. New York: Springer.

Grinin, L. E, Markov, A. V., Korotayev, A. V.

   2013. On Similarities between Biological and Social Evolutionary Mechanisms: Mathematical Modeling. Cliodynamics 4(2): 185–228.

   2014. Mathematical Modeling of Biological and Social Evolutionary Macrotrends. In Grinin, L., Korotayev, A. (eds.), History & Mathematics: Trends and Cycles. Volgograd: ‘Uchitel’ Publishing House, pp. 9–48.

   2015. Modeling of Biological and Social Phases of Big History. In Grinin, L. E., Korotayev, A. V. (eds.), Evolution: From Big Bang to Nanorobots. Volgograd: ‘Uchitel’ Publishing House, pp. 111–150.

Heidmann, J. 1989. Cosmic Odyssey. Cambridge: Cambridge University Press.

Hoerner, S. J. von. 1975. Population Explosion and Interstellar Expansion. Journal of the British Interplanetary Society 28: 691–712.

Huebner, J. 2005. A Possible Declining Trend for Worldwide Innovation. Technological Forecasting and Social Change 72(8): 980–986.

J. B. W. 1975. Paleozoic Era, Upper. The New Encyclopedia Britannica. 15^th ed. Vol. 13. Chicago: Encyclopedia Britannica, pp. 921–930.

Jaspers, K. 1955. Von Ursprung und Ziel der Geschichte. Frankfurt/Main: Fisher Bucherei.

Johansen, A., Sornette, D. 2001. Finite-Time Singularity in the Dynamics of the World Population and Economic Indices. Physica A 294(3–4): 465–502.

Johanson, D., Edgar, B. 1996. From Lucy to Language. New York: Simon and Schuster.

Jones, C. 2018. Aging, Secular Stagnation and the Business Cycle. N. p.: International Monetary Fund.

Jones, S. (ed.). 1994. The Cambridge Encyclopedia of Human Evolution. Cambridge: Cambridge University Press.

Kapitza, S. P.

   1996. The Phenomenological Theory of World Population Growth. Physics-uspekhi 39(1): 57–71.

   2003. The Statistical Theory of Global Population Growth. Formal Descriptions of Developing Systems. Dordrecht: Springer, pp. 11–35.

   2006. Global Population Blow-up and After. Hamburg: Global Marshall Plan Initiative.

   2010. On the Theory of Global Population Growth. Physics-uspekhi 53(12): 1287–1296.

Khaltourina, D. A., Korotayev, A. V. 2007. A Modified Version of a Compact Mathematical Model of the World System Economic, Demographic, and Cultural Development. In Dmitriev, M. G., Petrov, A. P. (eds.), Mathematical Modeling of Social and Economic Dynamics. Moscow: RUDN, pp. 274–277.

Khaltourina, D., Korotayev, A., Malkov, A. 2006. A Compact Macromodel of the World System Demographic and Economic Growth, 1–1973 CE. Cybernetics and Systems 1: 330–335.

Korotayev, A.

   2005. A Compact Macromodel of World System Evolution. Journal of World-Systems Research 11(1): 79–93.

  2006a. The World System History Periodization and Mathematical Models of Socio-historical Processes. In Grinin, L., de Munck, V. C., Korotayev, A. (eds.), History & Mathematics: Analyzing and Modeling Global Development. Moscow: KomKniga/URSS, pp. 39–98.

   2006b. The World System Urbanization Dynamics: A Quantitative Analysis. In Turchin, P., Grinin, L., de Munck, V. C., Korotayev, A. (eds.), History & Mathematics: Historical Dynamics and Development of Complex Societies. Moscow: KomKniga/URSS, pp. 44–62.

   2007a. Compact Mathematical Models of World System Development, and How they Can Help Us to Clarify Our Understanding of Globalization Processes. In Modelski, G., Devezas, T., Thompson, W. R., Globalization as Evolutionary Process: Modeling Global Change. London: Routledge, pp. 133–160.

   2007b. Secular Сycles and Millennial Trends: A Mathematical Model. In Dmitriev, M., Petrov, A. (eds.), Mathematical Modeling of Social and Econo-
mic Dynamics. Moscow: RUDN, pp. 118–125.

   2008. Globalization and Mathematical Modeling of Global Development. In Grinin, L. E., Beliaev, D. D., Korotayev, A. V. (eds.), Hierarchy and Power in The History Of Civilizations: Political Aspects Of Modernity. Moscow: LIBROCOM/URSS, pp. 225–240.

   2009. Compact Mathematical Models of the World System Development and Their Applicability to the Development of Local Solutions in Third World Countries. In Sheffield, J. (ed.), Systemic Development: Local Solutions in a Global Environment. Litchfield Park, AZ: ISCE Publishing, pp. 103−116.

   2012. Globalization and Mathematical Modeling of Global Development. Globalistics and Globalization Studies 1: 148–158.

   2013. Globalization and Mathematical Modeling of Global Evolution. In Grinin, L. E., Korotayev, А. V. (eds.), Evolution: Development within Big History, Evolutionary and World-System Paradigms. Volgograd: ‘Uchitel’ Publishing House, pp. 69–83.

   2018. The 21^st Century Singularity and its Big History Implications: A Re-analysis. Journal of Big History II(3): 71–118.

Korotayev, A., Goldstone, J., Zinkina, J. 2015. Phases of Global Demographic Transition Correlate with Phases of the Great Divergence and Great Convergence. Technological Forecasting and Social Change 95: 163–169.

Korotayev, A., Khaltourina, D. 2006. Introduction to Social Macrodynamics: Secular Cycles and Millennial Trends in Africa. Moscow: KomKniga/URSS.

Korotayev, A., Malkov, A., Khaltourina, D.

   2006a. Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth. Moscow: KomKniga/URSS.

   2006b. Introduction to Social Macrodynamics: Secular Cycles and Millennial Trends. Moscow: KomKniga/URSS.

Korotayev, A., Malkov, A. 2016. A Compact Mathematical Model of the World System Economic and Demographic Growth, 1 CE – 1973 CE. International Journal of Mathematical Models and Methods in Applied Sciences 10: 200–209.

Korotayev, A., Malkov, S. 2012. Mathematical Models of the World-system Development. Routledge Handbook of World-Systems Analysis. London: Routledge, pp. 158–161.

Korotayev, A. V., Markov, A. V.

   2014. Mathematical Modeling of Biological and Social Phases of Big History. In Grinin, L., Baker, D., Quaedackers, E., Korotayev, A. (eds.), Teaching & Researching Big History: Exploring a New Scholarly Field. Volgograd: ‘Uchitel’ Publishing House, pp. 188–219.

   2015. Mathematical Modeling of Biological and Social Phases of Big History. Globalistics and Globalization Studies 4: 319–343.

Korotayev, A., Zinkina, J. 2017. Systemic Boundary Issues in the Light of Mathematical Modeling of World-system Evolution. Journal of Globalization Studies 8(1): 78–96.

Kremer, M. 1993. Population Growth and Technological Change: One Million B.C. to 1990. The Quarterly Journal of Economics 108: 681–716.

Kurzweil, R.

   2001. The Law of Accelerating Returns. KurzweilAI.net 3-7-2001. URL: http://www.kurzweilai.net/articles/art0134.html?printable=1.

   2005. The Singularity is Near: When Humans Transcend Biology. New York: Viking Penguin.

LePoire, D. J.

   2005. Application of Logistic Analysis to the History of Physics. Technological Forecasting and Social Change 72(4): 471–479.

   2009. Exploration of Connections between Energy Use and Leadership Transitions. In Thompson, W. R. (ed.), Systemic Transitions: Past, Present, and Future. New York: Palgrave Macmillan, pp. 205–220.

   2013. Potential Economic and Energy Indicators of Inflection in Complexity. In Grinin, L. E., Korotayev, А. V. (eds.), Evolution: Development within Big History, Evolutionary and World-System Paradigms. Volgograd: ‘Uchitel’ Publishing House, pp. 108–118.

   2015. Interpreting “Big History” as Complex Adaptive System Dynamics with Nested Logistic Transitions in Energy Flow and Organization. Emergence: Complexity and Organization 17(1): 107–121.

   2016. Exploring Temporal Patterns in Big History Dynamics. KronoScope 16(2): 229–249.

Livi-Bacci, M. 2012. A Concise History of World Population. Chichester: Wiley-Blackwell.

Maddison, A.

   2001. Monitoring the World Economy: A Millennial Perspective. Paris: OECD.

   2007. Contours of the World Economy, 1–2030. Oxford: Oxford University Press.

Markov, A. V., Anisimov, V. A., Korotayev, A. V. 2010. Relationship between Genome Size and Organismal Complexity in the Lineage Leading from Prokaryotes to Mammals. Paleontological Journal 44(4): 363–373.

Markov, A. V., Korotayev, A. V.

   2007. Phanerozoic Marine Biodiversity Follows a Hyperbolic Trend. Palaeoworld 16(4): 311–318.

   2008. Hyperbolic Growth of Marine and Continental Biodiversity through the Phanerozoic and Community Evolution. Zhurnal obshchei biologii 69(3): 175–194.

McEvedy, C., Jones, R. 1978. Atlas of World Population History. New York, NY: Facts on File.

Modis, T.

   2002. Forecasting the Growth of Complexity and Change. Technological Forecasting and Social Change 69(4): 377–404.

   2003. The Limits of Complexity and Change. The Futurist 37(3): 26–32.

   2005. Discussion of Huebner Article Comments by Theodore Modis. Technological Forecasting and Social Change 72: 987–988.

   2012. Why the Singularity cannot Happen. In Eden, A. H., Moor, J. H., Søraker, J. H., Steinhart, E. (eds.), Singularity Hypothesis: A Scientific and Philosophical Assessment. Berlin: Springer, pp. 311–346.

Nazaretyan, A. P.

   2003. Power and Wisdom: Toward a History of Social Behavior. Journal of the Theory of Social Behaviour 33(4): 405–425.

   2005. Big (Universal) History Paradigm: Versions and Approaches. Social Evolution & History 4(1): 61–86.

   2015. Megahistory and its Mysterious Singularity. Herald of the Russian Academy of Sciences 85(4): 352–361.

   2016. Non-linear Futures: The “Mysterious Singularity” in View of Mega-History. Between Past Orthodoxies and the Future of Globalization. Contemporary Philosophical Problems. Boston: Brill-Rodopi, pp. 171–191.

   2017. Mega-History and the Twenty-first Century Singularity Puzzle. Social Evolution & History 16(1): 31–52.

   2018. The Polyfurcation Century: Does the Evolution on Earth have a Cosmological Relevance? Journal of Big History 2(1): 27–41.

Orgel, L. E. 1998. The Origin of Life – How Long did it Take? Origins of Life and Evolution of the Biosphere 28: 91–96.

Panov, A. D.

   2005. Scaling Law of the Biological Evolution and the Hypothesis of the Self-consistent Galaxy Origin of Life. Advances in Space Research 36(2): 220–225.

   2011. Post-singular Evolution and Post-singular Civilizations. In Grinin, L. E., Korotayev, А. V., Rodrigue, B. H. (eds.), Evolution: A Big History Perspective. Volgograd: ‘Uchitel’ Publishing House, 2011, pp. 212–231.

   2017. Singularity of Evolution and Post-Singular Development. In Grinin, L., Korotayev, A., Rodrigue, B. (eds.), From Big Bang to Galactic Civilizations. A Big History Anthology. Vol. III. The Ways that Big History Works: Cosmos, Life, Society and Our Future. Delhi: Primus Books, pp. 370–402.

Piketty, T. 2014. Capital in the Twenty-First Century. Cambridge, MA: The Belknap Press of Harvard University Press.

Podlazov, A. V. 2017. A Theory of the Global Demographic Process. Herald of the Russian Academy of Sciences 87(3): 256–266.

Popović, M. 2018. Technological Progress, Globalization, and Secular Stagnation. Journal of Central Banking Theory and Practice 7(1): 59–100.

Ranj, B. 2016. Google's Chief Futurist Ray Kurzweil Thinks We Could Start Living Forever by 2029. Business Insider April 20. URL: http://www.techinsider.io/googles-chief-futurist-thinks-we-could-start-living-forever-by-2029-2016-4.

Sagan, S. 1989. The Dragons of Eden: Speculations on the Evolution of Human Intelligence. New York: Ballantine Books.

Shanahan, M. 2015. The Technological Singularity. Cambridge, MA: MIT Press.

Schopf, J. W. (ed.). 1991. Major Events in the History of Life. Boston: Jones and Bartlett Publishers.

Snooks, G. D.

   1996. The Dynamic Society: Exploring the Sources of Global Change. London: Routledge.

   2005. Big History or Big Theory? Uncovering the Laws of Life. Social Evolution & History 4(1): 160–188.

Summers, L. H. 2016. The Age of Secular Stagnation: What it is and What to Do about it. Foreign Affairs 95(2): 2–9.

T. K. 1975. Paleozoic Era, Lower. The New Encyclopedia Britannica. 15^th ed. Vol. 13. Chicago: Encyclopedia Britannica, Inc., pp. 916–920.

Taagepera, R. 1976. Crisis around 2005 AD? A Technology-population Interaction Model. General Systems 21: 137–138.

Taylor, G., Tyers, R. 2017. Secular Stagnation: Determinants and Consequences for Australia. Economic Record 93(303): 615–650.

Teulings, C., Baldwin, R. (eds.). 2014. Secular Stagnation: Facts, Causes, and Cures. London: CEPR.

Tsirel, S. V. 2004. On the Possible Reasons for the Hyperexponential Growth of the Earth Population. In Dmitriev, M., Petrov, A. (eds.), Mathematical Modeling of Social and Economic Dynamics. Moscow: Russian State Social University, pp. 367–369.

UN Population Division. 2018. United Nations Population Division Database. New York: United Nations. URL: http://www.un.org/esa/population.

Wood, B. 1992. Origin and Evolution of the Genus Homo. Nature 355: 783–790.

---

* Исследование выполнено при поддержке Российского фонда фундаментальных исследований (проект № 17-02-00521а-ОГН).

[1] Напомним, что, по определению Международной ассоциации Большой истории, ее суть заключается в «стремлении понять интегрированную историю Космоса, Земли, Жизни и Человечества с использованием надежных эмпирических данных и научных методов» (https://bighistory.org/).

[2] О понятии пороговых вех Большой истории (Big History Thresholds) см.: Christian 2008. Стоит пояснить, что в качестве пятой пороговой вехи Большой истории Д. Кристиан рассматривает возникновение жизни, шестой – антропогенез и возникновение «коллективного обучения» (collective learning), седьмой – неолитическую революцию, а восьмой – глобальную модернизацию последних веков, особенно активно происходившую в XIX–XX веках (Modern Revolution).

[3] Собственно говоря, прототип этого графика (но в двойной логарифмической шкале) можно найти в опубликованном Курцвейлом в 2001 году эссе (Kurzweil 2001: 5).

[4] Точнее, это дата, когда, согласно последнему прогнозу Курцвейла, люди станут бессмертными, что вполне можно рассматривать как своего рода сингулярность (а также в качестве довольно вероятного кандидата на девятую пороговую веху Большой истории) – даже если мы действительно имеем дело с радикальным увеличением ожидаемой продолжительности жизни человека (или постчеловека?), а не с бессмертием как таковым, поскольку это все равно будет означать изменение биологической природы людей, что не может не повлиять на ход человеческой истории самым драматичным образом.

[5] Описанные ниже расчеты были впервые представлены в ноябре 2003 года на семинаре Государственного астрономического института в Москве (Nazaretyan 2005: 69) и впоследствии опубликованы в статьях (Панов 2004; 2005; 2006; Panov 2005; 2011; 2017) и монографии (Панов 2008: 19–40).

[6] Именно так (не без некоторых оснований) называет Т. Модис (Modis 2002; 2003) то, что А. Д. Панов обозначает как «биосферные революции» или «фазовые переходы».

[7] Т. Модис впервые представил свои результаты в 2002 году в статье (Modis 2002); эту статью А. Д. Панов прочитал только в марте 2018 года, т. е. через 15 лет после первого публичного представления его собственных результатов (см. выше).

[8] Собственно говоря, Модис начинает с Большого взрыва, но Курцвейл вполне обоснованно предпочитает начать с формирования Млечного Пути.

[9] По крайней мере, при составлении своего первого списка «фазовых переходов / биосферных революций» на русском языке (Панов 2004; 2005). Отметим, что при подготовке публикации своих результатов на английском языке Панов (Panov 2005) добавил к своей почти полностью русскоязычной библиографии восемь публикаций на английском (Begun 2003; Carroll 1988; Jones 1994; Nazaretyan 2003; A. H. 1975; A. P. 1975; J. B. W. 1975; T. K. 1975) и одну публикацию на немецком языке (Jaspers 1955). Нельзя полностью исключить того, что это могло как-то повлиять на датировку Пановым некоторых из его «биосферных революций» (действительно, можно найти – очень, впрочем, небольшие – различия в датировках между публикациями 2005 года на русском [Панов 2005] и английском [Panov 2005] языке). Отметим также, что эти англоязычные публикации включают в себя четыре статьи из Encyclopedia Britannica, что сделало список источников в англоязычной статье Панова (Ibid.) уже не столь тотально отличным от модисовского списка, как это наблюдалось для русскоязычной статьи (Панов 2005). Поэтому «для чистоты эксперимента» мы решили в наших вычислениях опираться на пановский список «фазовых переходов / биосферных революций», представленный в его русскоязычной, а не англоязычной статье.

[10] Отметим, что в тех случаях, когда Панов (2005) указывает временные интервалы, а не точные даты, мы для расчетов использовали средние значения соответствующих интервалов; например, Панов (Там же) в качестве даты «биосферной революции 5» («Начало неогена») указывает 25–20 × 10⁶ лет назад, в то время как мы для расчетов используем среднее значение соответствующего интервала (т. е. 22,5 × 10⁶ лет назад).

[11] Отмечу, что в статье С. В. Циреля (2018) обосновываются утверждения, что формулы, описывающие ряды Модиса – Курцвейла и Панова, по построению имеют показатель степени β = 1 и в силу практически полного совпадения начальной и двух конечных точек не могли существенно разойтись друг с другом, а небольшие различия значений числителя объясняются разным количеством фазовых переходов.

[12] Все вычисления приводятся ниже в миллионах человек. Отметим также, что использованное нами значение параметра C несколько отличается от значения, применявшегося фон Ферстером.

[13] См.: Марков, Коротаев 2007; 2008а; 2008б; 2008в; 2009а; 2009б; Марков и др. 2010; 2011; Коротаев 2007; 2010б; Коротаев, Марков 2006; Коротаев, Комарова, Халтурина 2007; Коротаев, Малков, Халтурина 2005б; Коротаев, Халтурина 2009; Korotayev 2005; 2006a; 2006b; 2007a; 2007b; 2008; 2009; 2012; 2013; Korotayev, Khaltourina 2006; Khaltourina et al. 2006; Korotayev, Malkov, Khaltourina 2006a; 2006b; Markov, Korotayev 2007; 2008; Markov, Anisimov, Korotayev 2010; Korotayev, Malkov 2012; Korotayev, Markov 2014; 2015; Grinin et al. 2013; 2014; 2015; Korotayev, Malkov 2016; Korotayev, Zinkina 2017.

[14] По крайней мере, А. П. Назаретян (2015а: 761) пишет о «завершающем фазовом переходе, сопоставимом по значению с появлением жизни».

[15] Демонстрируя вместе с тем, что обнаруживаемая сингулярность должна скорее служить индикатором перегиба, после которого темпы глобального макроэволюционного развития в долгосрочной перспективе начнут систематически замедляться.

[16] Между прочим, это очень близко к сингулярности 2005 года, которую мы ранее обнаружили при анализе ряда данных А. Мэддисона (Maddison 2001; 2007) по мировому ВВП за 1–1973 годы (Коротаев, Малков, Халтурина 2005а; 2005б; 2007; 2008; Korotayev, Malkov, Khaltourina 2006a; 2006b) и которую еще раньше в данных по мировому ВВП отметил Р. Таагепера (Taagepera 1976).

[17] Отметим, что наиболее ранняя из извеcтных нам попыток математически выявить Cингулярность на основе данных по человеческой истории была предпринята еще в 1909 году Г. Адамсом, который обнаружил ее в районе 1921 года при одном способе подсчетов, а при втором способе подсчетов – в районе 2025 года (Adams 1969 [1909]: 308), – что, конечно, совсем недалеко от демографической сингулярности 2027 года, выявленной Х. фон Ферстером в 1960 году, а также от планетарной сингулярности 2027 года, обнаруженной нами выше во временном ряду Панова.
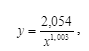