Human Values and Modernization: A Global Analysis
скачать Авторы:
- Korotayev, Andrey - подписаться на статьи автора
- Zinkina, Julia - подписаться на статьи автора
- Elena Slinko - подписаться на статьи автора
- Meshcherina, Kira - подписаться на статьи автора
Журнал: Journal of Globalization Studies. Volume 10, Number 1 / May 2019 - подписаться на статьи журнала
DOI: https://doi.org/10.30884/jogs/2019.01.04
We offer a world-wide analysis of the variation of human values with modernization. Ronald Inglehart and Christian Welzel, the authors of the Human Development Sequence Theory, suggest modernization to be one of the main processes forming the value structures in a population. The current paper investigates the relation between values and modernization applying some elements of the method proposed by Inglehart and Welzel to the data of Shalom Schwartz. The values survey by Schwartz specifies two main value axes, namely conservation/openness to change and self-transcendence/self-enhancement. Our research has revealed that the correlation between these two value axes differs in its direction when estimated for ‘macro-Europe’ (including Europe and former settlement colonies of North and South America and Oceania) and ‘Afrasia’ (including Asia and Africa). In the Western world there is a significant positive correlation between openness to change and self-transcendence, while in the Eastern world this correlation is strong, significant, and negative. We investigate the possible impact of modernization on this difference. To do this, we approximate modernization through such indicators as GDP per capita and the proportions of the labour force employed in various sectors of economy. We find that in both megazones modernization is accompanied by increasing openness to change. As for the self-transcendence/self-enhancement axis, we propose two possible explanations of the different dynamics observed in Europe and in ‘the East’ (Asia and North Africa), namely 1) that Eastern and Western societies find themselves at different modernization stages, and 2) different civilizational patterns. Further analysis makes the latter explanation look more plausible.
Keywords: global modernization, ‘macro-Europe’, ‘Afrasia’, human values, openness to change, Schwartz value axes, self-transcendence, GDP per capita, the West, the East.
Andrey Korotayev is Head and Professor of the Department of Modern Asian and African Studies more
Julia Zinkina is a specialist in the field of analysis of complex systems and processes more
Еlena Slinko more
Kira Meshcherina more
Introduction
This article contributes to the study of the dynamics of human values in the processes of modernization. The prominent scholars in the field of human values Inglehart and Welzel showed that the advancement of societies towards modernization is one of the main processes shaping the values of generations. The features of the development of society make impact on the values in childhood, adolescence and youth and these values form the sociocultural image of society when these generations reach maturity (see Inglehart and Welzel 2005).
We examine the correlation between values and modernization using some elements of Inglehart and Welzel's methods (where indicators such as GDP per capita and proportions of the population employed in various sectors of the economy serve as proxy variables for modernization), but we do not use the value indexes of Inglehart and Welzel, but of Schwartz. In his research Schwartz identifies two main value axes: conservation/openness to change and self-transcendence/self-enhancement (see Materials and Methods). The most noteworthy result is that the correlation between these two value axes differs in its directions in the ‘macro-European’ megazone (including the countries of Europe and the former settlement colonies of North and South America and Oceania) and the ‘Afrasian’ megazone (i.e. Asia + Africa). In both cases, the correlation turns out to be strong, but in ‘macro-Europe’ it is negative (i.e. an increase in openness to change is accompanied by a decline in self-enhancement values), and in ‘Afrasia’ the correlation is positive (i.e. an increase in openness to change is accompanied by an increase in self-enhancement). In this article, we study the relationship of both value axes with modernization indices and put forward two hypotheses that help to explain the opposing directions of the correlation in these megazones.
Analytic Framework
Modernization is by no means the only trajectory of the human development that influences the value structure of the societies. Therefore, the question is whether the collapse of the USSR and the ensuing economic instability, unemployment, crime, etc. can be considered as a step on the way to modernization, is very controversial. However, there is no doubt that this historical period had a strong influence on the formation of the value pattern (and the picture of the world as a whole) of Soviet generations. Nevertheless, globally, modernization remains one of the key factors affecting the value patterns of the population in different countries. The human development sequence theory proposed by Inglehart and Welzel describes this fact.
Their theory is based on a factor analysis of several waves of the World Values Survey, which identified two main components. One of them is defined as the axis of religious values versus secular values (explains the most part of the variation), the second axis is survival values versus self-expression values. The processes of value modernization according to Inglehart and Welzel's theory takes place in two phases (these main components and their weights are listed in Appendix 1). In the first phase, there is a transition from traditional religious values to secular values, linked with the theory of a transition from an agrarian society to an industrial phase. In the second phase of modernization (the transition from the industrial to the postindustrial society), there is a shift along the second axis, from survival values to self-expression values (see Inglehart and Welzel 2005; Welzel, Inglehart and Klingemann 2003; Welzel and Inglehart 2005; Welzel 2013).
However, on closer examination, these value axes raise a number of questions. Regarding the first axis there is a controversial fact of mixing state integration and religious integration. For example, is it possible to consider that a sense of national pride has some religious connotations? Moreover, it should be remembered that the emergence of modern national statehood (as well as feelings of nationalism) is the result of the modernization of the early modern times, in other words, the deviation from traditional societies. As for the second axis, the question here is the inclusion of the subjective level of happiness. First, the inclusion of such an indicator in the list of values is ambiguous. Second, there is a possibility that the results of the correlation analysis conducted by Inglehart and Welzel (according to the data of the 1990s) were influenced by the situation in Post-Communist countries, where a particularly high percentage of people claimed that they had a low level of happiness (see, for example, Korotayev and Khaltourina 2009: 142−159). The situation in these countries has changed quite noticeably, and the results of the correlation analysis require rechecking on new data.
The theory of the human development sequence is fundamentally materialistic, since economic development is the main determinant of value changes. Industrialization provides a transition from traditional religious to secular values and the further growth of GDP per capita. Material abundance causes a gradual shift towards post-materialistic values. Moreover, this theory postulates that it is through values that the economic development influences democratization. As economic progress proceeds, a transition to self-expression values and emancipation takes place and the desire to manage one's own life creates a motivation for demanding more democracy (see Inglehart and Welzel 2005; Welzel et al. 2012; Welzel, Inglehart and Klingemann 2003; Welzel and Inglehart 2005; Welzel 2013).
However, this provision has been criticized in a number of studies (Hadenius and Teorell 2005; Teorell and Hadenius 2006; Teorell 2010; Spaiser et al. 2014; Dahlum and Knutsen 2016). For example, in a recent paper (Spaiser et al. 2014) it was shown that the trigger of both democratization and the emancipation of the population is the achievement of a critical level of the Human Development Index, while democratization based on human rights precedes a growth of emancipation values, and not the other way around. Other research work (Dahlum and Knutsen 2016) emphasizes the cross-national correlations between self-expression values and democracy identified by Inglehart and Welzel, may not result from a causal relationship between these phenomena, but from other processes. Dahlum and Knutsen show that self-expression values do not raise either the level of democracy or the likelihood of democratization, and do not stabilize existing democracies, quite the opposite, the experience of democracy increases self-expression values. Having regard to the above, we decided to re-verify Inglehart and Welzel's theory on the connection between values and modernization but using the data of Schwartz.
Materials and Methods
One of the most developed theories of human values is Schwartz's theory (see Schwartz 1992, 1994, 2006a, 2006b; Schwartz and Bardi 1997; Schwartz and Boehnke 2004; Schwartz et al. 2001, 2012), which seeks to identify the basic value orientations by which every individual is guided, regardless of his cultural affiliation. The basic ten value classification includes values of Power, Achievement, Hedonism, Stimulation, Self-Direction, Universalism, Benevolence, Tradition, Conformity and Security. These values are grouped into four blocks: Conservation values (Security, Conformity and Tradition), Openness to Change values (Self-Direction, Stimulation and Hedonism), and Self-Transcendence values (Universalism and Benevolence) and Self-Enhancement values (Power, Achievement and Hedonism). The four blocks form a space of values, consisting of two axes: Conservation – Openness to Change values and Self-Transcendence – Self-Enhancement values.
The complete questionnaire of Schwartz consists of two parts. The first includes 57 items such as nouns and adjectives describing values (equality, pleasure, etc.); so a respondent during the survey assesses the importance of these values. The second is the so-called personality profile, which consists of 40 statements describing a person in accordance with the above-mentioned ten basic value types. In this part of the survey, the respondent is asked to assess how much the described person is similar to him. The Schwartz's questionnaire was used to collect data for several projects, one of which is the World Values Survey (WVS). WVS is a comparative value study that was started in 1981 with the goal of providing researchers with cross-country data on values and preferences. The study is conducted in almost 100 countries around the world on a nationally representative sample. Simultaneously with WVS, a similar European study, EVS (European Values Survey), was conducted in 49 countries before 2008. EVS also included questions from the Schwartz's questionnaire, which were identical to questions in WVS project. Therefore, for the purposes of our study, we have combined data from these two bases.
Tests
1. Correlations between the Schwartz's axes for different world macrozones
We begin our analysis by examining how the indices of value axes conservation/openness correlate to change and self-transcendence/self-enhancement – initially for all world macrozones, then at the zonal levels. It does not appear possible to detect any unified pattern between the main Schwartz's value axes at the global level and the correlation between them turns out to be weak and insignificant (see Fig. 1).
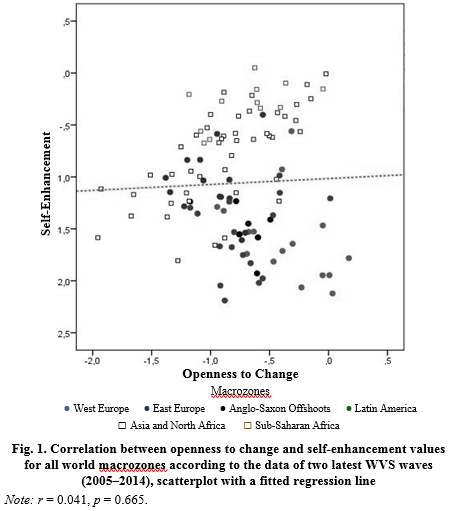
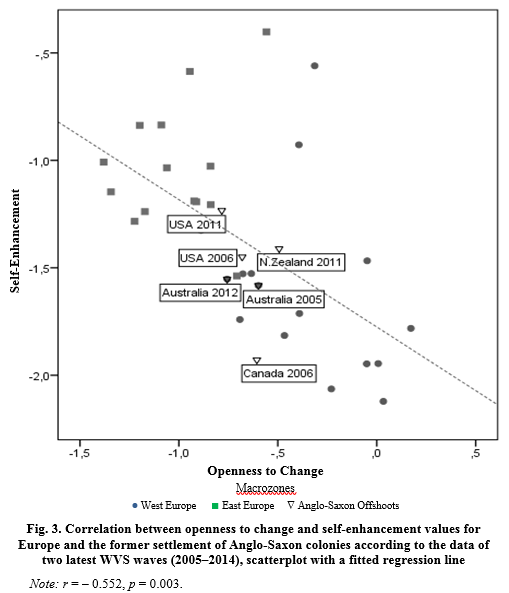
Latin America's cluster fits quite well into the European cluster. It forms a particularly close cluster with the former Anglo-Saxon settlement colonies that leads to formation of a single macrocluster of the former European settlement colonies of America, Australia and New Zealand. This macrocluster in its turn combines with the West European and East European clusters to form a single ‘macro-European’ megacluster, which unites all European countries and all former European settlement colonies.
2. Schwarz's value axes and indicators of modernization
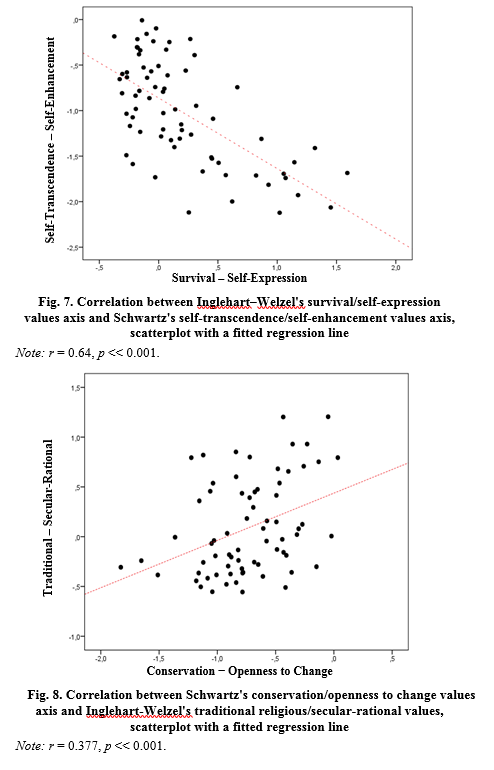
Note that Schwartz's value axes have not a strong but a statistically significant correlation with value axes used by Inglehart and Welzel (2005). They are traditional religious/secular-rational values and survival/self-expression values. Herewith, Schwartz's openness to change values shows not a strong but a statistically significant positive correlation with Inglehart – Welzel's secular-rational values, and Schwartz's self-enhancement values show not a strong, but a statistically significant negative correlation with Inglehart – Welzel's self-expression values (see Figs 7 and 8).
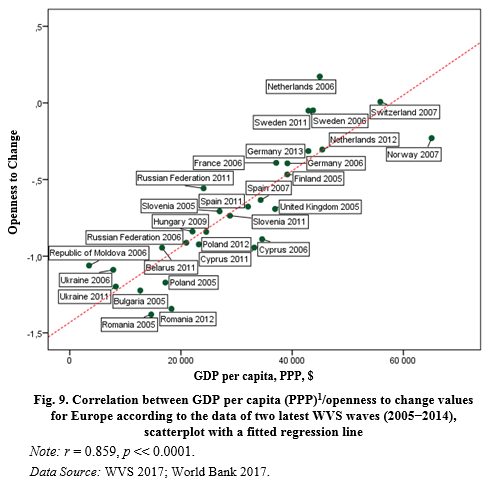
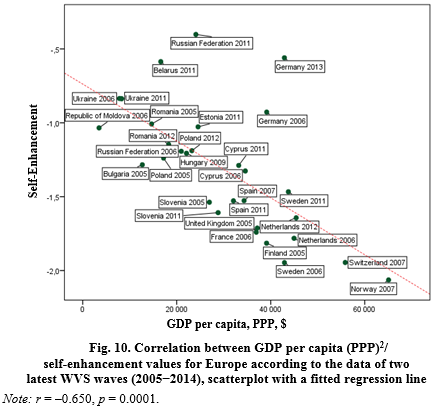
Given this, we can expect that openness to change values will show a positive correlation with GDP per capita and self-enhancement values – a negative one. We begin our empirical test of this hypothesis on the data of European countries. When using this data, there are strong correlations in the predicted directions as in relating to openness to change values (see Fig. 9), as well as in relating to self-enhancement values (see Fig. 10).
As mentioned, according to Inglehart and Welzel's theory, the value modernization involves two phases. At the first phase (transition from an agrarian society to an industrial one), there is a transition from traditional to secular-rational values. They confirm this hypothesis using a correlation analysis which showed that in the wake of rising differences between the proportion employed in industry and in agriculture, there is a decline in the prevalence of traditional religious values and a growth in the prevalence of secular-rational values.
According to this theory, the shift from survival to self-expression values occurs in the second phase of global modernization, during the transition from an industrial to a postindustrial society. They confirm this hypothesis also using a correlation analysis which showed that an increase in the differences between the proportions employed in service and industry is accompanied by a decline in the prevalence of survival values and a growth in the prevalence of self-expression values that again fully corresponds to the main points of the Inglehart-Welzel's hypothesis.
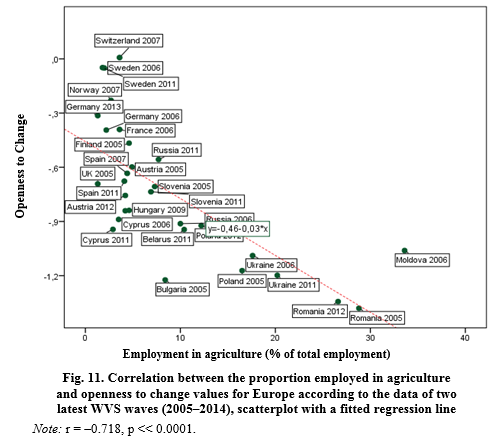
The empirical test of this hypothesis provided inconclusive results. Neither Schwartz's openness to change values nor Schwartz's self-enhancement values show any statistically significant correlation with the proportion employed in industry. However, in accordance with the theoretical expectations for the European countries openness to change values demonstrated a strong negative correlation with the proportion employed in agriculture (see Fig. 11). As would be expected according to Inglehart – Welzel's theory the proportion employed in agriculture shows a positive correlation with self-enhancement values, but this correlation is not as strong as a negative correlation between the proportion employed in agriculture and openness to change values (see Fig. 12).
Employment in agriculture (% of total employment)
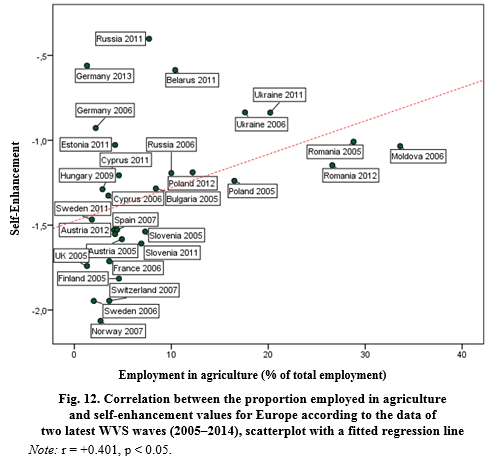
The less modernized societies in Europe with a large proportion employed in agriculture are characterized by a significantly higher prevalence of self-enhancement values and a significantly less importance of self-transcendence values (as well as protection for nature).On the other hand, self-enhancement values demonstrated a theoretically predicted statistically significant negative correlation with the difference between the proportion employed in the service sector and industry (r = –0.477, p < 0.05).
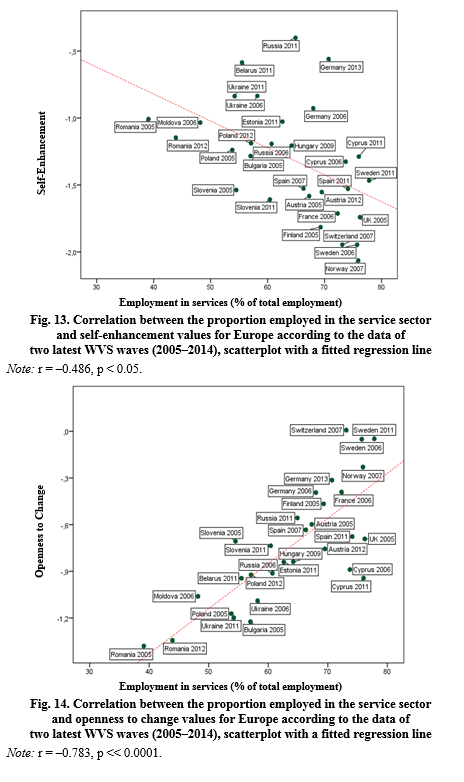
The negative correlation between the non-calibrated proportion employed in the service sector and self-enhancement values is almost as strong and statistically significant (see Fig. 13). The positive correlation between the proportion employed in the service sector and the prevalence of openness to change values is even stronger and statistically significant (see Fig. 14).
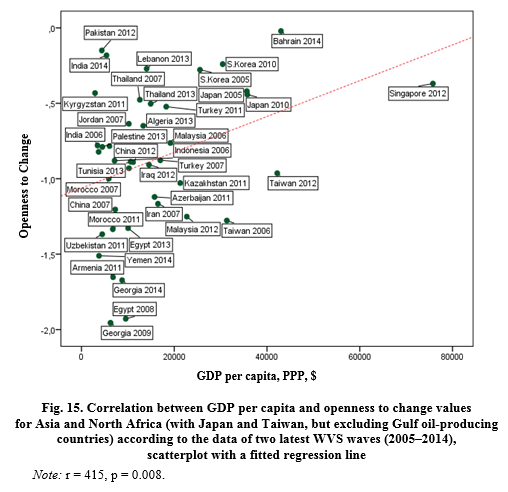
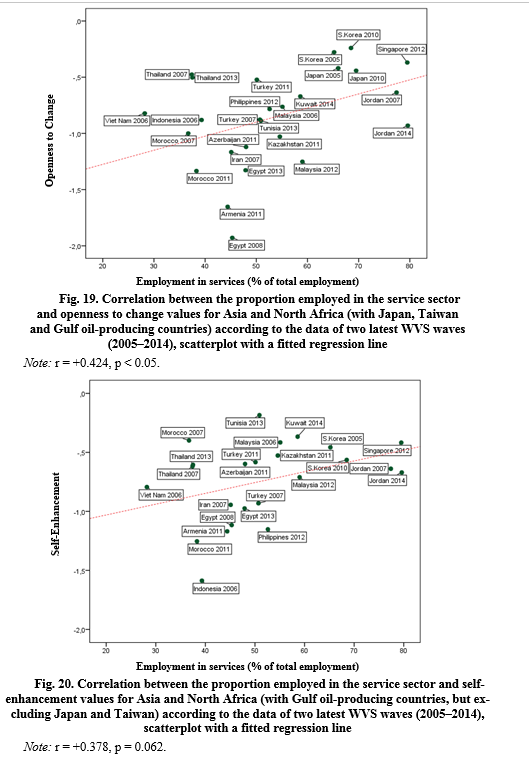
Indeed, like in Europe, for the East we find a marginally significant negative correlation between the proportion employed in agriculture and the prevalence of openness to change values (see Fig. 17).
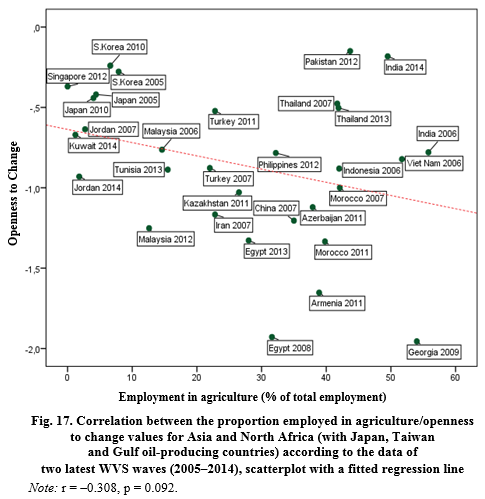
Employment in agriculture (% of total employment)
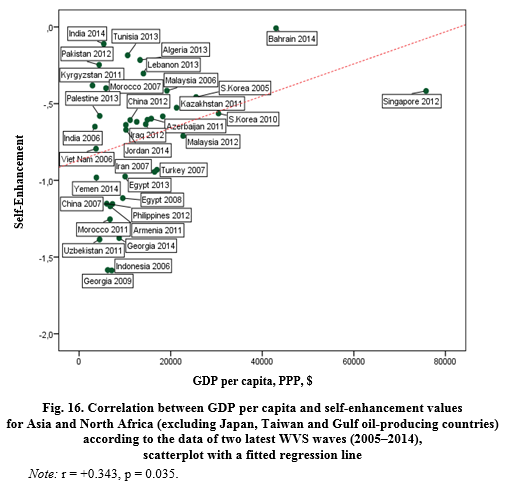
But in Europe the proportion of employed in agriculture positively correlates with the prevalence of self-enhancement values, while in Asia and North Africa we are dealing with marginally significant negative correlation (see Fig. 18). Reducing the proportion employed in agriculture is one of the most important components of modernization processes (see, e.g., Black 1967).
Thus, a statistically significant negative correlation between employed in agriculture and self-enhancement values that we observed in the East (against the background of the positive correlation in Europe) can be regarded as additional support for the above-formulated hypothesis maintaining that in Europe modernization tends to decrease of prevalence of self-enhancement values whereas in Asia and North Africa modernization tends to be accompanied by an increase in prevalence of self-enhance-
ment values.
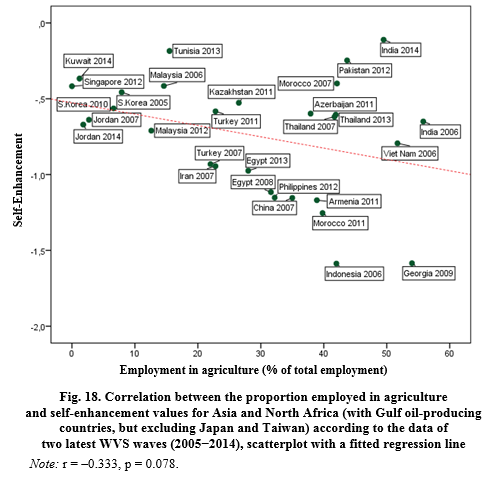
Employment in agriculture (% of total employment)
Similar results are obtained in the correlation analysis of openness to change self-enhancement values with the proportion employed in the service sector. Openness to change in the East (as well as in Europe [see Fig. 14 above]) shows a positive correlation with the proportion employed in the service sector (see Fig. 19). However, self-enhancement values also show a positive correlation for Asia and North Africa (seeFig. 20) while for Europe the correlation is negative (see Fig. 13).
Thus, if in Europe there is a negative correlation between the proportion employed in the service sector and self-enhancement values, in Asia and North Africa we are dealing with a positive correlation. This can be regarded as another empirical verification of the hypothesis put forward above: although either in Europe or in Asia and North Africa the modernization as a trend leads to an increase in the prevalence of openness to change values, only in the East the modernization leads to a growth of self-enhancement values. At the same time, in Europe modernization processes are accompanied not by a growth, but by a decline in the prevalence of self-enhancement values.
Thus, we are dealing with essentially different patterns of value modernization both in Europe and in the East. What factors might explain this? Below we will consider two possible explanations.
1) ‘Stadial or phase explanation’. The opposing directions of the correlations between openness to change and self-enhancement values for Europe and the East can be explained by the fact that most of Asian and North African countries are at much earlier phases of the modernization transition than in most European countries. This suggests that an increasing openness to change values is observed hroughout the modernization transition, and an increase in self-enhancement values occurs only in its earlier phases, while in its later phases the further development of social systems leads to a decline in the prevalence of self-enhancement values.
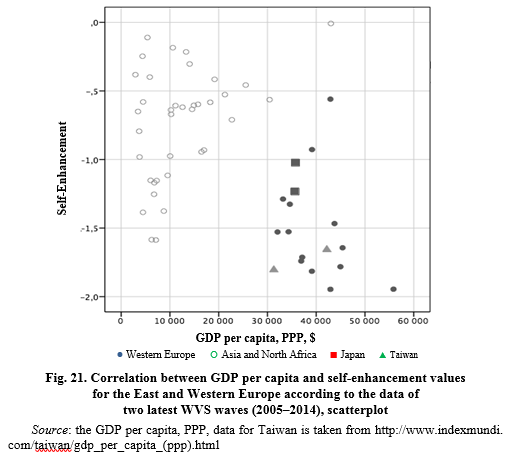
This explanation is supported by the fact that in the most modernized social systems in Asia, like Japan and Taiwan, there are quite low levels of self-enhancement values like in highly developed Western European countries, compared to middle income Asian countries (see Fig. 21).
However, there is an additional factor. In the vast majority of countries younger age groups have higher indices of openness to change values as well as self-enhancement values (see, e.g., Robinson 2013). Most Afrasian countries have a very young population compared to Europe, which would seem to explain why in these countries there are much higher indices of both value types mentioned above and which would not be expected according to the level of modernization in these countries. It would seem that this factor could explain why in the Afrasian countries there is a correlation between these two value types, which is directly opposing to the correlation seen in ‘Old’ Europe. Nevertheless, the preliminary analysis has shown that these results obtained can explain the difference in the correlation patterns between the Europe and the Afrasian world to an unexpectedly small extent. More details of our respective tests will be presented in our next article.
Conclusion
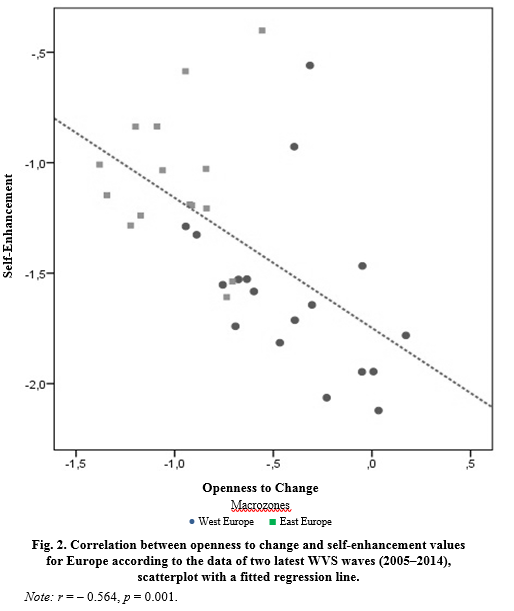
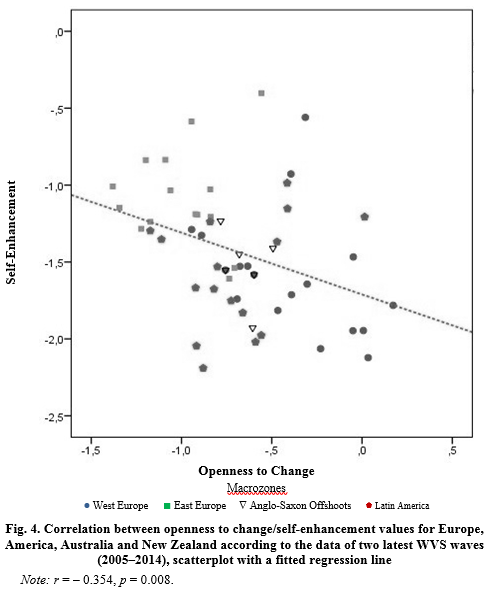
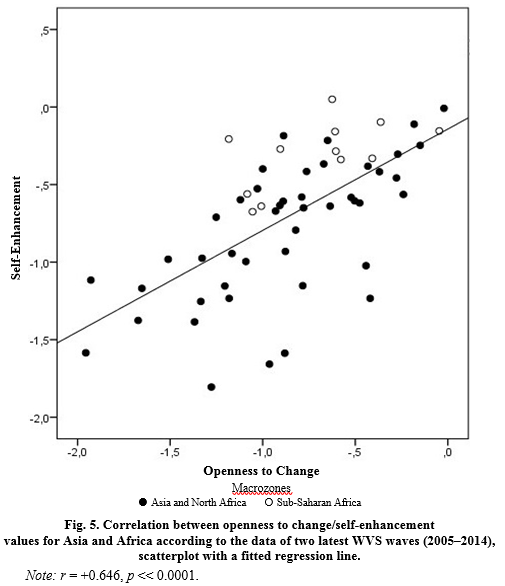
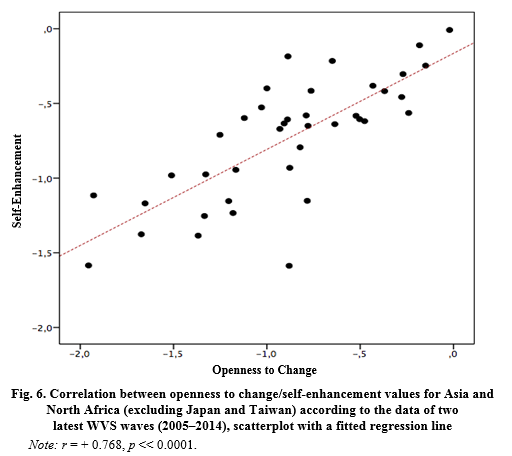
Thus, our analysis divides the whole world into two human value megazones. The macro-European megazone, which includes not only all European countries, but all former European colonies in America and Oceania, is characterized by a pronounced negative correlation between openness to change and self-enhancement values (see Fig. 4. r = –0.354, p = 0.008). This correlation is especially strong for Europe (see Fig. 2. r = –0.564, p = 0.001). The Afrasian megazone, which consists of all countries in Asia and Africa, is characterized by a pronounced positive correlation between openness to change and self-enhancement values (see Fig. 5. r = + 0.646, p << 0.0001), while it is especially strong for Asia and North Africa4 (see Fig. 6. r = +0.768, p << 0.0001).
In both megazones, modernization (approximated by such indicators as GDP per capita and proportions of employment in various sectors of economy) is accompanied by a decline in conservation values and an increasing openness to change values, but in the macro-European megazone, the growth of openness to change values is accompanied by a growth of self-transcendence values, while in Afrasia – by an increase in self-enhancement values. We propose two hypotheses that allow explaining the opposing directions of the correlations in these megazones and they are 1) different modernization stages and 2) different civilizational patterns. The further analysis shows that the difference between Europe and the Eastern world can only partially be explained via the phase factor and to a large extent, it seems, we are dealing with the difference in civilizational patterns of the value modernization.
NOTES
* This research has been supported by the Russian Science Foundation (Project No. 18-18-00254).
1 In 2011 international dollars at PPPs.
2 In 2011 international dollars at PPPs.
3 Excluding a Russian case and this is just the exception that confirms the rule.
4 Excluding the most westernized Asian countries.
REFERENCES
Black, C. E. 1967. The Dynamics of Modernization: A Study in Comparative History. New York, NY: Harper & Row.
Dahlum, S., and Knutsen, C. H. 2016. Democracy by Demand? Reinvestigating the Effect of Self-Expression Values on Political Regime Type. British Journal of Political Science 47: 1−25.
Hadenius, A., and Teorell, J. 2005. Cultural and Economic Prerequisites of Democracy: Reassessing Recent Evidence. Studies in Comparative International Development 39: 87–106.
Inglehart, R., and Welzel, C. 2005. Modernization, Cultural Change, and Democracy: The Human Development Sequence. Cambridge: Cambridge University Press.
Korotayev, A., and Khaltourina, D. 2009. Modern Trends of World Development. Moscow: Librokom/URSS. Original in Russian (Коротаев А., Халтурина Д. Современные тенденции мирового развития. М.: Либроком/УРСС).
Kuznets, S., and Murphy, J. T. 1966. Modern Economic Growth: Rate, Structure, and Spread. New Haven, CT: Yale University Press.
Schwartz, S. H. 1992. Universals in the Content and Structure of Values: Theory and Empirical Tests in 20 Countries. In Zanna, M. (ed.), Advances in Experimental Social Psychology. Vol. 25 (pp. 1−65). New York: Academic Press. http://dx.doi.org/10.1016/S0065-2601(08)60281-6
Schwartz, S. H. 1994. Are there Universal Aspects in the Content and Structure of Values? Journal of Social Issues 50: 19−45. URL: http://dx.doi.org/10.1111/ j.15404560.1994.tb01196.x.
Schwartz, S. H. 1996. Value Priorities and Behavior: Applying a Theory of Integrated Value Systems. In Seligman, C., Olson, J. M., and Zanna, M. P. (eds.), The Psychology of Values: The Ontario Symposium. Vol. 8 (pp. 1−24). Hillsdale, NJ: Erlbaum.
Schwartz, S. H. 2006a. Les valeurs de base de la personne: Théorie, mesures et applications [Basic Human Values: Theory, Measurement, and Applications]. Revue Française de Sociologie 47: 249−288.
Schwartz, S. H. 2006b. Value Orientations: Measurement, Antecedents and Consequences across Nations. In Jowell, R., Roberts, C., Fitzgerald, R. and Eva, G. (eds.), Measuring Attitudes Cross-nationally − Lessons from the European Social Survey (pp. 169−203). London, UK: Sage.
Schwartz, S. H., and Bardi, A. 1997. Influences of Adaptation to Communist Rule on Value Priorities in Eastern Europe. Political Psychology 18: 385−410. URL: http://dx.doi.org/10.1111/0162-895X.00062.
Schwartz, S. H., and Boehnke, K. 2004. Evaluating the Structure of Human Values with Confirmatory Factor Analysis. Journal of Research in Personality 38: 230−255. URL: http://dx.doi.org/10.1016/S0092-6566(03)00069-2.
Schwartz, S. H., Cieciuch, J., Vecchione, M., Davidov, E., Fischer, R., Beierlein, C., Ramos, A., Verkasalo, M., Lönnqvist, J.-E., Demirutku, K., Dirilen-Gumus, O., and Konty, M. 2012. Refining the Theory of Basic Individual Values. Journal of Personality and Social Psychology 103: 663−688. URL: http://dx.doi.org/10.1037/a0029393.
Schwartz, S. H., Melech, G., Lehmann, A., Burgess, S., and Harris, M. 2001. Extending the Cross-Cultural Validity of the Theory of Basic Human Values with a Different Method of Measurement. Journal of Cross-Cultural Psychology 32: 519−542. URL: http://dx.doi.org/10.1177/0022022101032005001.
Solow, R. M. 1956. A Contribution to the Theory of Economic Growth. The Quarterly Journal of Economics 70 (1): 65–94.
Spaiser, V., Ranganathan, S., Mann, R. P., and Sumpter, D. J. 2014. The Dynamics of Democracy, Development and Cultural Values. PloS one 9 (6), e97856.
Teorell, J., and Hadenius, A. 2006. Democracy without Democratic Values: A Rejoinder to Welzel and Inglehart. Studies in Comparative International Development 41 (3): 95–111.
Teorell, J. 2010. Determinants of Democratization: Explaining Regime Change in the World, 1972–2006. Cambridge: Cambridge University Press.
Welzel, C. 2013. Freedom Rising. Human Empowerment and the Quest for Emancipation. Cambridge: Cambridge University Press.
Welzel, C., and Inglehart, R. 2005. Liberalism, Postmaterialism, and the Growth of Freedom. International Review of Sociology 15 (1): 81–108.
Welzel, C., Inglehart, R., Aleksander, E., and Ponarin, E. D. 2012. Disentangling the Links between Culture and Institutions on the Example of the Emancipation of the Humanity. Zhurnal sotsiologii i sotsial'noy antropologii 15 (4): 12–43. Original in Russian (Велцель К., Инглхарт Р., Александер Э., Понарин Э. Д. Распутывание связей между культурой и институтами на примере эмансипации человечества. Журнал социологии и социальной антропологии 15 (4): 12–43).
Welzel, C., Inglehart, R., and Klingemann, H. D. 2003. The Theory of Human Development: A Cross-Cultural Analysis. European Journal of Political Research 42: 341–379.
Appendix 1
Traditional values emphasize the following
(Secular-Rational values emphasize the opposite):
God is very important in respondent's life 0.91
It is more important for a child to learn obedience and religious faith than independence and determinations (Autonomy index) 0.88
Abortion is never justifiable 0.82
Respondent has strong sense of national pride 0.81
Respondent favors more respect for authority 0.73
Survival values emphasize the following
(Self-Expression values emphasize the opposite):
Respondent gives priority to economic and physical security over self-expression and quality-of-life (4-item Materialist/Postmaterialist Values Index) 0.87
Respondent describes self as not very happy 0.81
Homosexuality is never justifiable 0.7
Respondent has not signed and would not sign a petition 0.74
You have to be very careful about trusting people 0.46
Source: Inglehart and Welzel 2005: 49.
Appendix 2
Schwartz's value axes were formed on the basis of respondents' answers to the following questions in 2011:
V70. It is important to this person to think up new ideas and be creative; to do things one's own way.
V71. It is important to this person to be rich; to have a lot of money and expensive things.
V72. Living in secure surroundings is important to this person; to avoid anything that might be dangerous.
V73. It is important to this person to have a good time; to ‘spoil’ oneself.
V74. It is important to this person to do something for the good of society.
V75. Being very successful is important to this person; to have people recognize one's achievements.
V76. Adventure and taking risks are important to this person; to have an exciting life.
V77. It is important to this person to always behave properly; to avoid doing anything people would say is wrong.
V78. Looking after the environment is important to this person; to care for nature and save life resources.
V79. Tradition is important to this person; to follow the customs handed down by one's religion or family.
In 2006 respondents were asked a similar block of questions, but the formulation of one of them sounded differently: It is important for this people to help the people nearby; to care for their well-being.





