Systemic Boundary Issues in the Light of Mathematical Modeling of World-System Evolution
скачать Авторы:
- Korotayev, Andrey - подписаться на статьи автора
- Zinkina, Julia - подписаться на статьи автора
Журнал: Journal of Globalization Studies. Volume 8, Number 1 / May 2017 - подписаться на статьи журнала
In this article we demonstrate why mathematical models of the World System evolution are so important for the world-systems research, in general, and for the issue of systemic boundaries in particular. The point is that those mathematical models demonstrate in a rather convincing way that in order that a certain set of human societies would demonstrate systemic qualities (and – thus – could be described with a single mathematical model), it is sufficient that just one condition is observed – it is necessary that the technological innovations made in one society of a system could diffuse within a millennium throughout all the other societies of the system. As soon as this condition is satisfied, the respective set of human societies can be treated as a single system (and – what is important – can be described with a single mathematical model), and we do not know any better designation for such a system than the ‘world-system’. This, of course suggests rather specific criteria for the world-systemic boundaries.
Keywords: systemic boundaries, technology, Afroeurasian world-system, mathematical modeling, demography, population, history of globalization, the World System, domesticates.
In this article we will attempt to demonstrate why mathematical models of the World System evolution are so important for the world-systems research in general, and for the issue of systemic boundaries in particular. We will try to show that these models suggest a novel approach to the world-systems research allowing perceiving the issue of the systemic boundaries in a new light.
* * *
In 1960, von Foerster, Mora, and Amiot published, in the journal Science, a striking discovery. They showed that between 1 and 1958 CE the world's population (N) dynamics can be described in an extremely accurate way with an astonishingly simple equation:1

where Nt is the world population at time t, and C and t0 are constants, with t0 corresponding to an absolute limit (‘singularity’ point) at which N would become infinite.
Parameter t0 was estimated by von Foerster and his colleagues as 2026.87, which corresponds to November 13, 2026; this made it possible for them to supply their article with a public-relations masterpiece title – ‘Doomsday: Friday, 13 November, A.D. 2026’ (von Foerster, Mora, and Amiot 1960).2
Note that the graphic representation of this equation is nothing but a hyperbola; thus, the growth pattern described is denoted as ‘hyperbolic’.
Note that the von Foerster equation, 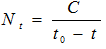
 .
.This equation can be also written as
 .
.where 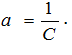
What is the meaning of this mathematical expression, ? In our context dN/dt denotes the absolute population growth rate at a certain moment of time. Hence, this equation states that the absolute population growth rate at any moment of time should be proportional to the square of population at this moment.
The main mathematical models (Taagepera 1976, 1979, 2014; Kremer 1993; Cohen 1995; Podlazov 2000, 2001, 2002, 2004; Tsirel 2004; Korotayev 2005, 2006, 2007, 2008, 2012; Korotayev, Malkov, and Khaltourina 2006a: 21–36; Korotayev, Malkov 2016) of the world population hyperbolic growth are based on the two following assumptions:
1) ‘the Malthusian (1978) assumption that population is limited by the available technology, so that the growth rate of population is proportional to the growth rate of technology’ (Kremer 1993: 681–682).3 This statement looks quite convincing. Indeed, throughout most of human history the world population was limited by the technologically determined ceiling of the carrying capacity of land. For example, with foraging subsistence technologies the Earth could not support more than 10 million people, because the amount of naturally available useful biomass on this planet is limited, and the world population managed to grow beyond this limit only when people started to apply various means to artificially increase the amount of available biomass, that is with the transition from foraging to food production. However, the extensive agriculture also can only support a limited number of people, and further growth of the world population only became possible with the intensification of agriculture and other technological improvements (see, e.g., Turchin 2003; Korotayev, Malkov, and Khaltourina 2006a, 2006b; Korotayev and Khaltourina 2006).
This assumption can be modeled in a number of ways. For example, Sergey Tsirel (2004) chooses for this purpose the classical logistic model of Pierre François Verhulst:

where K is the technologically determined carrying capacity of the Earth (as regards the humans).
However, as is well known, the technological level is not a constant, but a variable (see, e.g., Grinin 2006, 2007). And in order to describe its dynamics the second basic assumption is employed:
2) ‘High population spurs technological change because it increases the number of potential inventors…4 In a larger population there will be proportionally more people lucky or smart enough to come up with new ideas’ (Kremer 1993: 685), thus, ‘the growth rate of technology is proportional to total population’.5 In fact, here Kremer uses the main assumption of the Endogenous Technological Growth theory (Kuznets 1960; Grossman and Helpman 1991; Aghion and Howitt 1992, 1998; Simon 1977, 1981, 2000; Komlos and Nefedov 2002; Jones 1995, 2003, 2005 etc.). As this supposition, to our knowledge, was first proposed by Simon Kuznets (1960), we shall denote the corresponding type of dynamics as ‘Kuznetsian’,6 while the systems in which the ‘Kuznetsian’ population-technological dynamics is combined with the ‘Malthusian’ demographic one will be denoted as ‘Malthusian-Kuznetsian’. In general, we find this assumption rather plausible – in fact, it is quite probable that, other things being equal, within a given period of time, one billion people will make approximately one thousand times more inventions than one million people.
This assumption is expressed mathematically in the following way:
 .
.Actually, this equation just proves that the absolute technological growth rate at a given moment of time is proportional to the technological level observed at this moment (the wider is the technological base, the more inventions could be made on its basis), and, on the other hand, it is proportional to the population (the larger is the population, the larger is the number of potential inventors).7
As has been demonstrated on a number of occasions, when those two assumptions are expressed mathematically (e.g., in the way indicated above) and the two respective equations are united into a single mathematical system, the resultant mathematical model turns out to be capable of describing the global population growth in an extremely accurate way (Taagepera 1976, 1979; Kremer 1993; Podlazov 2000; Tsirel 2004; Korotayev 2005, 2012; Korotayev, Malkov, and Khaltourina 2006a: 21–36).
The resultant models provide a rather convincing explanation of why throughout most of human history the world population followed the hyperbolic pattern with the absolute population growth rate tending to be proportional to N2. For example, why will the growth of population from, say, 10 million to 100 million, result in the growth of dN/dt by 100 times? The above mentioned models explain this rather convincingly. The point is that the growth of world population from 10 to 100 million implies that human technology also grew approximately by ten times (given that it will have proven, after all, to be able to support a ten times larger population). On the other hand, the tenfold population growth also implies a tenfold growth of the number of potential inventors, and, hence, a tenfold increase in the relative technological growth rate. Hence, the absolute technological growth rate will grow 10 × 10 = 100 times (as, in accordance with equation (5), an order of magnitude larger number of people having at their disposal an order of magnitude wider technological basis would tend to make two orders of magnitude more inventions). And as N tends to the technologically determined carrying capacity ceiling, we have good reason to expect that dN/dt will also grow just by about 100 times.
In fact, it can be demonstrated (see, e.g., Korotayev, Malkov, and Khaltourina 2006a, 2006b; Korotayev and Khaltourina 2006) that the hyperbolic pattern of the world's population growth could be accounted for by the nonlinear second order positive feedback mechanism that was shown long ago to generate just the hyperbolic growth, known also as the ‘blow-up regime’ (see, e.g., Kurdjumov 1999; Knyazeva and Kurdjumov 2005). In our case this nonlinear second order positive feedback looks as follows: the more people – the more potential inventors – the faster technological growth – the faster growth of the Earth's carrying capacity – the faster population growth – with more people you also have more potential inventors – hence, faster technological growth, and so on (see Fig. 1).
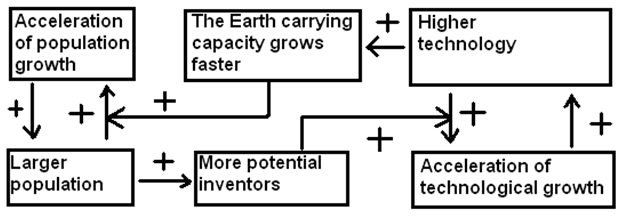
Note that the relationship between technological development and demographic growth cannot be analyzed through any simple cause-and-effect model, as we observe a true dynamic relationship between these two processes – each of them is both the cause and the effect of the other.
It is remarkable that this model suggests ways to answer one of the main objections raised against the hyperbolic models of the world's population growth. Indeed, at present the academic social science community has not accepted the mathematical models of world population growth as a hyperbolic one.8 We believe that there are substantial reasons for such a position, and that the authors of the respective models are as much to blame for this rejection as are social scientists.
Indeed, all these models are based on an assumption that world population can be treated as a system remaining integrated for many centuries, if not millennia, before 1492. Already in 1960, von Foerster, Mora, and Amiot spelled out this assumption in a rather explicit way,
However, what may be true for elements which, because of lack of adequate communication among each other, have to resort to a competitive, (almost) zero-sum multiperson game may be false for elements that possess a system of communication which enables them to form coalitions until all elements are so strongly linked that the population as a whole can be considered from a game-theoretical point of view as a single person playing a two-person game with nature as its opponent (von Foerster, Mora, and Amiot 1960: 1292).
However, did, for example, in 1–1500 CE, the inhabitants of, say, Central Asia, Tasmania, Hawaii, Terra del Fuego, the Kalahari etc. (i.e. just the world population) really have ‘adequate communication’ to make ‘all elements… so strongly linked that the population as a whole can be considered from a game-theoretical point of view as a single person playing a two-person game with nature as its opponent’? For any historically-minded social scientist the answer to this question is perfectly clear and, of course, it is squarely negative. Against this background it is hardly surprising that those social scientists who have happened to come across hyperbolic models for world population growth have tended to treat them merely as ‘demographic adventures of physicists’ (note that indeed, nine out of twelve currently known authors of such models are physicists); none of the respective authors (von Foerster, Mora, and Amiot 1960; von Hoerner 1975; Taagepera 1976, 1979; Kapitza 1992, 1999; Kremer 1993; Cohen 1995; Podlazov 2000, 2001, 2002, 2004; Johansen and Sornette 2001; Tsirel 2004), after all, has provided any convincing answer to the question above.
However, it is not so difficult to provide such an answer.
But before let us consider why the mathematical models of the World System evolution are so important for the world-systems research, in general, and for the issue of systemic boundaries in particular. The point is that those mathematical models demonstrate in a rather convincing way that in order that a certain set of human societies would demonstrate systemic qualities (and – thus – could be described with a single mathematical model) it is sufficient that just one condition is observed – it is necessary that the technological innovations made in one society of a system could diffuse within a millennium throughout all other societies of the system. As soon as this condition is satisfied, the respective set of human societies can be treated as a single system (and – what is important – can be described with a single mathematical model), and we do not know any better designation for such a system than the ‘world-system’. This, of course suggests rather specific criteria for the world-systemic boundaries. The boundary of any particular world-system can be identified via defining the zone of diffusion of the main technological innovations within a respective world-system. Thus the contacts between Central Asia and China in the 3rd and 2nd millennia BCE can be said to have resulted in the incorporation of China into the Afroeurasian world-system (the World System) as they led to the borrowing on the part of China of major technological innovations of the western part of Afroeurasia (wheat, barley, cattle, sheep, goats, horses, bronze metallurgy, wheeled transport, plow and so on), whereas the Norse contacts with the New World in the early 2nd millennium CE did not result in any changes of the world-system boundaries, as those contacts (unlike the Columbian ones) did not result in any significant diffusions of technologies either from Europe to the New World or from America to the Old World.
The hyperbolic trend observed for the world population growth after 10,000 BCE does appear to be primarily a product of the growth of quite a real system, a system that seems to have originated in West Asia around that time in direct connection with the Neolithic Revolution. With Andre Gunder Frank (1990, 1993; Frank and Gills 1994), we denote this system as ‘the World System’ (see also, e.g., Modelski 2000, 2003; Devezas and Modelski 2003). As has been just mentioned, the presence of the hyperbolic trend itself indicates that the major part of the entity in question had some systemic unity, and the evidence for this unity is readily available. Indeed, we have evidence for the systematic spread of major innovations (domesticated cereals, cattle, sheep, goats, horses, plow, wheel, copper, bronze, and later iron technology, and so on) throughout the whole North African – Eurasian Oikumene for a few millennia BCE (see, e.g., Chubarov 1991, or Diamond 1999 for a synthesis of such evidence).
Below we will consider some of this evidence in more detail.
One of the earliest examples of diffusion through the information network of the World System is the spread of domesticated plants and animals from their initial location of domestication. Several such locations are currently known (see Table 1), the most ancient one with the greatest number of domestications being the Near East. The so-called Near Eastern founder crop package includes emmer wheat, einkorn wheat, barley, pea, lentil, chickpea, bitter vetch, and one technical plant, namely linen9 (Zohary and Hopf 2000: 241–242). These primary domesticates spread wide from the Near East across the Central and Southern Asia about 8,000 BP (Zohary and Hopf 2000) and reached the major part of Europe about 7,000 BP (Brown et al. 2009: 108).
Table 1
Approximate domestication dates for the basic cultivars (crops and starches)
| Species | Domestication time, BP |
| Southwest Asia | |
| Emmer wheat, einkorn wheat, barley | 11,500–10,000 |
| Rye | 10,00010 |
| China | |
| Millet | 11,000 (Yang et al. 2012) – 8,000 |
| Rice | 9,000 (Molina et al. 2011; Liu et al. 2007) – 8,000 |
| Soya beans | 9,000 – 8,600 |
| Buckwheat | 8,000 (Ohnishi 1998; Amézqueta 2013) – 5,500 (Li et al. 2009) |
| Mexico | |
| Corn | 9,000 – 7,000 |
| South America | |
| Sweet potato | 10,000 – 8,000 (Roullier et al. 2013) |
| Manioc | 8,000 |
| Potato | 7,000 |
| New Guinea | |
| Yam, banana, taro | 7,000 (Denham et al. 2003; Perrier et al. 2011) |
| Africa | |
| Sorghum | 4,000 |
Source: Price and Bar-Yosef 2011: 170–171 unless stated otherwise in the footnotes.
Let us consider the spread of some of the cultivars mentioned in Table 1 in more detail. The geographic diffusion of the emmer wheat was tightly related to human migration. The Balkan and Asiatic groups of wheat come from south-western Anatolia, whereas the European group originates from Levant (Badaeva et al. 2015: 13–14). Cytogenetic analysis reveals four main ways of wheat diffusion throughout the Afroeurasian world-system:
– the ‘Balkan way’ goes from south-eastern Anatolia to the Balkans, and further on to the Eastern Europe, the Volga region, and the Urals;
– the ‘Asian way’ also starts in south-eastern Anatolia and goes through Transcaucasia and the Volga region into Europe; another ‘branch’ of this way passes Iran on to South Asia and India;
– the ‘European way’ starts in Southern Levant and goes through the Iberian Peninsula to Europe; archeological evidence supports the existence of two waves of agricultural diffusion into Europe, the first passing Turkey, the Balkans, and Central Europe up the river systems into Western Europe, and the second going through the seas into Southern Europe;
– the fourth way starts in Iran and Iraq to pass Oman, and therefrom to get to Ethiopia and India (Badaeva et al. 2015: 13–17).
Along with wheat, barley was domesticated in the Near East about 10,500 BP (Zohary and Hopf 2000; Diamond 2002). However, currently there is enough evidence to support the hypothesis that the domestication of barley occurred more than once (Morrell and Clegg 2007; Jones et al. 2013). Research on the difference in haplotype frequency reveals two centers of barley domestication, one in the Fertile Crescent, and one 1,500–3,000 km further to the East, probably in Zagros mountains or even further to the East (Morrell and Clegg 2007; Saisho and Purugganan 2007), probably in Tibet (see Dai et al. 2012; Ren et al. 2013). The barley domesticated in the Fertile Crescent contributed the majority of diversity in European and American cultivars. The second domestication contributed most of the diversity in barley from Central Asia to the Far East (Morrell and Clegg 2007; Saisho and Purugganan 2007).
Another independent center of domestication (nearly as ancient as the Fertile Crescent one) existed in China. Millet, rice, soya beans, and later on buckwheat were all domesticated in the territory of modern China (Yang et al. 2012). Among these cultures, the greatest impact on the global nutrition landscape belongs to rice. Rice was domesticated around 9,000 BP (Molina et al. 2011; Liu et al. 2007). Currently the most recent archeological and genetic research localizes rice domestication in the Lower Yangtze river valley (for a substantial review see Gross and Zhao 2014), and recognizes a later separate domestication in Africa11 (Vaughan, Lu, and Tomooka 2008; Li, Zheng, and Ge 2011; Molina et al. 2011; Huang et al. 2012). Rice domestication in India has been under great discussion until recently, the main question being whether there was another separate domestication of rice in this country (apart from the two domestication mentioned above). The latest genetic research shows that though rice domestication started separately in the Lower Yangtze valley and in India, in the latter this process finalized only after the fully domesticated rice from the former had reached it (Fuller 2011; Huang et al. 2012; Gross and Zhao 2014).
Let us now briefly view the history of the diffusion of domesticated rice across the Afro-Eurasian World System. About 5,000–4,500 BP domesticated rice went up the Yangtze river, reaching Sichuan and later on Yunnan (Fuller 2011). Around 4,500 BP this cultivar reached Taiwan and spread further to the south, both into coastal and inner regions of South-Eastern Asia. In India the first evidence of the presence of Chinese domesticated rice can be traced back to the epoch of Harappa (4,500–4,000 BP)12, Around 4,000–3,000 BP domesticated rice reached Japan and Korea (Gross and Zhao 2014).
Having reached India and South-East Asia, rice spread further on to the Near East (about 3,000 BP) and diffused from Persia to many regions of the Persian Empire; Europeans got to know rice thanks to Alexander the Great's campaign in India (Chang 2000).
As regards animal domestication, the major part of the modern diversity in domesticated animals goes up to one or several (but very few) initial domestication localities, wherefrom they gradually diffused through the World System. Thus, mitochondrial DNA analysis (supporting earlier archeological data) shows that almost all domesticated goats descend from Eastern Anatolia and northern and central Zagros (Naderi et al. 2008; see Zeder and Hesse 2000). As for pig domestication, mitochondrial DNA analysis localizes it in the Near East about 10,500 BP. Later on (about 6,000 BP) domesticated pigs reached Europe through two ways: via the Danube and the Rhine river valleys into the northwestern Europe, and via the southern sea way into the Mediterranean region (Larson et al. 2007, 2010). Simultaneously, Europe started to domesticate its own wild pig population, and rather soon these domesticated pigs prevailed on the Near Eastern ones (Larson et al. 2007).
For many years scientists have been discussing the ways how domesticates reached new regions – whether they came with new settlers, or it was information exchange between various population groups (i.e. the information networks of the ancient World System) that transferred new knowledge on domestication of various species. Currently there exists enough scientific evidence to support both hypotheses (Zeder 2011: 202). Thus, the diffusion of emmer wheat is strongly linked to human migration, whereas, for example, the diffusion of domesticated pigs looks much more like an information exchange.
Diffusion of technologies
The technological space of the World System before the Silk Road was relatively small as compared to later periods. However, the sustenance of the increasingly complex agrarian societies, chiefdoms, temple communities, early states, and later on agrarian empires, was based on a set of constantly improved technologies. Sets of technologies existed in production of luxury and bulk goods, construction, land and sea transportation etc. Some basic technologies of the ancient World System (such as pottery production) were independently invented in a number of different places (Kuzmin 2013); other technologies, say, in metallurgy (smelting of copper, bronze, and iron) and warfare (chariots) had a single place of invention, wherefrom they diffused throughout the World System. Let us view these two examples in greater detail.
Copper, bronze, and iron metallurgy
Scholars unanimously agree on the fundamental role of metallurgy in the sociopolitical and socioeconomic development of the ancient societies.
The emergence of early metal production, including mining, smelting and exchange, can be seen as a key element in the development of more complex social and political orders in the ancient world … Metal production marked an important transition towards increasing regional and interregional trade and the innovation and diffusion of new technologies, and routinely provided the material setting for wealth accumulation among emerging elite factions within early societies … Such conditions have been seen as contributing to the development of early ranked societies in Eurasia … and the rise and expansion of early states and empires from the fourth to early second millennia BC in the Near East (Hanks and Doonan 2009: 329–330).
Copper. The earliest evidence of the usage of natural copper and copper-based minerals appears in the Near East and Iran in 14,000 – 13,000 BP; copper becomes widely used in these regions in 10,000 – 9,000 BP (for a review see Killick and Fenn 2012: 562). However, the first evidence for copper smelting – the real start of copper metallurgy – is currently found in two regions, Iran, dating from 7,500 BP (Frame 2004: 1; Thornton 2009: 308), and Serbia, dating from 7,000 BP (Radivojević et al. 2010, 2013). By 6,000 BP copper metallurgy spread into east Turkey, southern Levant, and Central Europe (Roberts, Thornton, and Pigott 2009: 1014). As regards the spread of metallurgy from the Near East into the Far East, two most likely ways are suggested in literature, both starting in Anatolia and Iran. One way goes through the Caucasus and Eurasian steppe, the other passes the Amu-Darya river, Tianshan, and Kashgar (Tylecote 1976: 14; Linduff and Mei 2009: 275).
Bronze. The earliest tin-smelted bronze (found in the mountainous west of Iran) dates back to 6,000–5,000 BP. Around 5,000 BP the technology of tin-bronze smelting spread from here into Sumer, Arabia, the Mediterranean, then further on to Central Asia and Central Europe, and even to China (Darling 2002: 59–60; Roberts, Thornton, and Pigott 2009: 1015–1016). South-Eastern Asia received this technology via its contacts with the population of the Yellow and Yangtze river valleys (Higham et al. 2011: 227). Thus, all these regions appear to be part of a united network of information exchanges covering the whole of Eurasia.
Iron. Smelting iron ore was first carried out by the Hittites living in Anatolia about 3,500 BP (Headrick 2009: 36). Initially iron was inferior to bronze in terms of cracking and rusting, but superior to it thanks to the abundance of iron ore deposits and, consequently, relative cheapness of iron tools and weapons. In 3,200 BP, after the collapse of Hittite empire, the technology of iron ore smelting spread among the Near Eastern societies. Around 3,000 BP it got from Mesopotamia to India, in 2,800 BP from Arabia to Ethiopia, in 2,700 to Egypt and China, where it was substantially improved (Headrick 2009: 36–37).
Thus, all three technologies of metallurgy described above diffused through the World System very fast, reaching rather remote areas in just several centuries. In our opinion, this can be taken as a valid proof of the existence of a substantial information network tying together the World System far before the Silk Road came to existence.
Invention and diffusion of the war chariots
In the words of Russian historian Chechushkov: ‘Chariot complex is one of the most large-scale historical phenomena, geographically spreading in the vast territories of Eurasia, and chronologically embracing a major part of the Bronze Age’ (Chechushkov 2011: 62). The role of wheeled vehicles in ancient Eurasia was huge (especially among the pastoralists). Not only did they serve as the main means of transportation, but also were widely used in warfare (Hudyakov 2002: 139).
The earliest usage of two-wheeled vehicles is documented for the Near East in the third millennium BCE (Chechushkov 2011: 63). However, these vehicles were still far from light war chariots. A number of innovations was required, first of all, spoked wheel (instead of the earlier cross-bar wheels), and the domestication of horse (to replace donkeys). Thus, chariots as a whole technological complex appear in the Near East only in the seventeenth and sixteenth centuries BCE, when Egypt was conquered by the Hyksos (Chechushkov 2011: 63).
The prime of chariots and a rapid spread of this complex technology chariot starts around 3,600 BP. In just a little more than a century the light chariots spread throughout the territory stretching from Greece to India, from Russia to southern Egypt (Moorey 1986: 196). The massive use of chariots is recorded about 1457 BCE in the Battle of Megiddo. Around 3,200 BP the chariot technology reached China (Shaughnessy 1988). The speed of spread of a rather sophisticated technology and a close similarity of the forms of chariots on the entire Eurasian territory point to the diffusion of this technology (as opposed to the multiple inventions). Moreover, it is commonly hypothesized that this spread has been associated with a particular group of people (Indo-Aryans) (Moorey 1986: 196).
As a result, the evolution of societies of the Afroeurasian world-system (= the World System) already at this time cannot be regarded as truly independent. By the end of the first millennium BCE we observe a belt of cultures, stretching from the Atlantic to the Pacific, with an astonishingly similar level of cultural complexity characterized by agricultural production of wheat and other specific cereals, the breeding of cattle, sheep, and goats; use of the plow, iron metallurgy, and wheeled transport; development of professional armies and cavalries deploying rather similar weapons; elaborate bureaucracies, and Axial Age ideologies, and so on – this list could be extended for pages. A few millennia before, we would find another belt of societies strikingly similar in level and character of cultural complexity, stretching from the Balkans up to the Indus Valley outskirts (Peregrine and Ember 2001: vols 4 and 8; Peregrine 2003). Note that in both cases, the respective entities included the major part of the contemporary world's population (see, e.g., McEvedy and Jones 1978; Durand 1977 etc.). We would interpret this as a tangible result of the World System's functioning. The alternative explanations would involve a sort of miraculous scenario that these cultures with strikingly similar levels and character of complexity somehow developed independently of each other in a very large but continuous zone, while for some reason nothing comparable to them appeared elsewhere in other parts of the world, which were not parts of the World System. We find such an alternative explanation highly implausible.
Thus, we would tend to treat the world population's hyperbolic growth pattern as reflecting the growth of quite a real entity – of the World System.
A few other points seem to be relevant here. Of course, there would be no grounds for speaking about a World System stretching from the Atlantic to the Pacific, even at the beginning of the first millennium CE, if we applied the ‘bulk-good’ criterion suggested by Wallerstein (1974, 1987, 2004), as there was no movement of bulk goods at all between, say, China and Europe at this time (as we have no reason to disagree with Wallerstein in his classification of the first century Chinese silk reaching Europe as a luxury rather than a bulk good). However, the first century CE (and even the first millennium BCE) World System definitely qualifies as such if we apply the ‘softer’ information-network criterion suggested by Chase-Dunn and Hall (1997). Note that at our level of analysis the presence of an information network covering the whole World System is a perfectly sufficient condition, which makes it possible to consider this system as a single evolving entity. Yet, in the first millennium BCE any bulk goods could hardly penetrate from the Pacific coast of Eurasia to its Atlantic coast. However, the World System had reached by that time such a level of integration that iron metallurgy could spread through the whole of the World System within a few centuries.
Of course, in the millennia preceding the European colonization of Tasmania its population dynamics – oscillating around the 4000 level (e.g., Diamond 1999) – were not influenced by World System population dynamics and did not influence it at all. However, such facts just suggest that since the tenth millennium BCE the dynamics of the world population reflect very vividly the very dynamics of the World System population.
Conclusion
We believe that the theory specified above can shed a new light on the issue of systemic boundaries. It could be suggested that within a new approach the main emphasis would be moved to the generation and diffusion of innovations. If a society borrows systematically important technological innovations, its evolution already cannot be considered as really independent, but should rather be considered as a part of a larger evolving entity, within which such innovations are systematically produced and diffused. The main idea of the world-system approach was to find the evolving unit. The basic idea was that it is impossible to account for the evolution of a single society without taking into consideration that it was a part of a larger whole. However, traditional world-system analysis concentrated on bulk-good movements, and core – periphery exploitation, thoroughly neglecting the above-mentioned dimension. Meanwhile, the technological innovations diffusion network turns out to be the oldest mechanism of the world-systems integration, and remained extremely important throughout the whole history, remaining important up to the present. It seems to be even more important than the core – periphery exploitation (e.g., without taking this mechanism into consideration it appears impossible to account for such things as the twentieth-century demographic explosion whose proximate cause was the dramatic decline of mortality, but whose main ultimate cause was the diffusion of innovations produced almost exclusively within the world-system core). This also suggests a redefinition of the world-system core. The core is not the world-system zone exploiting other zones, but rather it is the zone with the highest innovation donor/recipient ratio, the principal innovation donor.
The mathematical models specified above demonstrate in a rather convincing way that in order that a certain set of human societies would demonstrate systemic qualities (and – thus – could be described with a single mathematical model) it is sufficient that just one condition is observed – it is necessary that the technological innovations made in one society within a system could diffuse within a millennium throughout all the other societies of the system. As soon as this condition is satisfied, the respective set of human societies can be treated as a single system (and – what is important – can be described with a single mathematical model), and we do not know any better designation for such a system than the ‘world-system’. This, of course suggests rather specific criteria for the world-systemic boundaries. The boundary of any particular world-system can be identified by regarding the zone within which the main technological innovations made within the respective world-system diffused. Thus the contacts between Central Asia and China in the third and second millennia BCE can be said to have resulted in the incorporation of China into the Afroeurasian world-system as they led to the borrowing on the part of China of major technological innovations of the western part of Afroeurasia (wheat, barley, cattle, sheep, goats, horses, bronze metallurgy, wheeled transport, plow and so on), whereas the Norse contacts with the New World in the early second millennium CE did not result in any changes of the world-system boundaries, as those contacts (unlike the Columbian ones) did not result in any significant diffusions of technologies either from Europe to the New World or from America to the Old World.
Acknowledgement
This research has been supported by the Russian Science Foundation (project No. 15-18-30063).
1 To be exact, the equation proposed by von Foerster and his colleagues looked as follows: 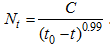
.
2 Of course, von Foerster and his colleagues did not imply that the world population on that day could actually become infinite. The real implication was that the world population growth pattern that was followed for many centuries prior to 1960 was about to come to an end and be transformed into a radically different pattern. Note that this prediction began to be fulfilled only in a few years after the ‘Doomsday’ paper was published, starting from 1960 the world population growth began to diverge more and more from the blow-up regime, and now it is not hyperbolic any more (see, e.g., Korotayev, Malkov, and Khaltourina 2006a, where we present a compact mathematical model that describes both the hyperbolic development of the World System in the period prior to the early 1970s, and its withdrawal from the blow-up regime in the subsequent period).
3 In addition to this, the absolute growth rate is proportional to the population itself – with a given relative growth rate a larger population will increase more in absolute numbers than a smaller one.
4 ‘This implication flows naturally from the non-rivalry of technology… The cost of inventing a new technology is independent of the number of people who use it. Thus, holding constant the share of resources devoted to research, an increase in population leads to an increase in technological change’ (Kremer 1993: 681).
5 Note that ‘the growth rate of technology’ means here a relative growth rate (i.e. the level to which technology will grow in a given unit of time in proportion to the level observed at the beginning of this period).
6 In Economic Anthropology it is usually denoted as ‘Boserupian’ (see, e.g., Boserup 1965; Lee 1986).
7 Taagepera, Kremer, Podlazov, and Tsirel did not test this hypothesis empirically in a direct way. Note, however, that our own empirical test of this hypothesis has supported it (see Korotayev, Malkov, and Khaltourina 2006b: 141–146).
8 The title of an article by a social scientist discussing Kapitza's model – Demographic Adventures of a Physicist [Shishkov 2005] – is rather telling in this respect.
9 Triticum dicoccum Schübl., Triticum monococcum L., Hordeum vulgare L., Pisum sativum L., Lens culinaris Medik., Cicer arietinum L., Vicia ervilia (L.) Willd., Linum usitatissimum L.
10 In Abu-Hureira the first examples of rye with phenotypical features of domestication belong to 12,500 BP (Hillman et al. 2001).
11 Domestication of African rice is localized in Sahel, Upper Niger (Li, Zheng, and Ge 2011).
12 About 4,000 BP a number of other Chinese species reach the north-western regions of India and Pakistan, such as peach, apricot, millet, etc. (Fuller 2011).
Aghion, P., and Howitt, P. 1992. A Model of Growth through Creative Destruction. Econometrica 60: 323–352.
Aghion, P., and Howitt, P. 1998. Endogenous Growth Theory. Cambridge, MA: MIT Press.
Amézqueta, S., Galán, E., Vila-Fernández, I., Pumarola, S., Carrascal, M., Abian, J., ... and Torres, J. L. 2013. The Presence of D-Fagomine in the Human Diet from Buckwheat-Based Foodstuffs. Food Chemistry 136 (3): 1316–1321.
Badaeva, E. D., Keilwagen, J., Knüpffer, H., Waßermann, L., Dedkova, O. S., Mitrofanova, O. P., ... and Kilian, B. 2015. Chromosomal Passports Provide New Insights into Diffusion of Emmer Wheat. PloS one 10 (5), e0128556.
Boserup, E. 1965. The Conditions of Agricultural Growth: The Economics of Agrarian Change under Population Pressure. Chicago, IL: Aldine.
Brown, T. A., Jones, M. K., Powell, W., and Allaby, R. G. 2009. The Complex Origins of Domesticated Crops in the Fertile Crescent. Trends in Ecology and Evolution 24 (2): 103–109.
Chang, T.-T. 2000. Rice. In K. F. Kiple, K. C. Ornelas (eds.), The Cambridge World History of Food, vol. 1 (pp. 132–148). Cambridge: Cambridge University Press.
Chase-Dunn, C., and Hall, T. D. 1997. Rise and Demise: Comparing World-Systems. Boulder, CO: Westview Press.
Chechushkov, I. V. 2011. Chariots of the Eurasian Steppe in the Bronze Epoch. Vestnik arheologii, antropologii i etnografii 2 (15): 57–65. In Russian (Чечушков И. В. Колесницы евразийских степей эпохи бронзы. Вестник археологии, антропологии и этнографии 2 (15): 57–65).
Chubarov, V. V. 1991. The Near-Eastern Locomotive: The Tempos of Development of Technique and Technology in the Ancient World. In Korotayev, A. V., and Chubarov, V. V. (eds.), The Archaic Society: The Main Problems of Sociology of Development. Vol. 1 (pp. 92–135). Moscow: Institute of History of the USSR of AN USSR. In Russian (Чубаров В. В. Ближневосточный локомотив: темпы развития техники и технологии Древнего мира. Архаическое общество: Узловые проблемы социологии развития, т. 1 / Ред. А. В. Коротаев, В. В. Чубаров, с. 92–135. М.: Институт истории СССР Академии Наук СССР).
Cohen, J. E. 1995. Population Growth and Earth's Carrying Capacity. Science 269 (5222): 341–346.
Dai F., Nevo, E., Wu, D., Comadran, J., Zhou, M., Qiu, L., ... and Zhang, G. 2012. Tibet is One of the Centers of Domestication of Cultivated Barley. Proceedings of the National Academy of Sciences 109 (42): 16969–16973.
Darling, A. S. 2002. Non-Ferrous Metals. In McNeil, I. (ed.), An Encyclopaedia of the History of Technology (pp. 47–145). London, New York: Routledge.
Denham, T. P., Haberle, S. G., Lentfer, C., Fullagar, R., Field, J., Therin, M., ... and Winsborough, B. 2003. Origins of Agriculture at Kuk Swamp in the Highlands of New Guinea. Science 301 (5630): 189–193.
Devezas, T., and Modelski, G. 2003. Power Law Behavior and World System Evolution. Technological Forecasting and Social Change 70: 819–859.
Diamond, J. 2002. Evolution, Consequences and Future of Plant and Animal Domestication. Nature 418 (6898): 700–707.
Diamond, J. 1999. Guns, Germs, and Steel: The Fates of Human Societies. New York: Norton.
Durand, J. D. 1977. Historical Estimates of World Population: An Evaluation. Population and Development Review 3 (3): 255–296.
Foerster, H. von, Mora, P., and Amiot, L. 1960. Doomsday: Friday, 13 November, A. D. 2026. At this Date Human Population will Approach Infinity if it Grows as it has Grown in the Last Two Millennia. Science 132: 1291–1295.
Frame, L. L. D. 2004. Investigations at Tal-i Iblis: Evidence for Copper Smelting during the Chalcolithic Period. Doctoral Dissertation, Massachusetts Institute of Technology.
Frank, A. G. 1990. A Theoretical Introduction to 5,000 Years of World System History. Review 13 (2): 155–248.
Frank, A. G. 1993. The Bronze Age World System and its Cycles. Current Anthropology 34: 383–413.
Frank, A. G., and Gills, B. 1994. (Eds.) The World System: 500 or 5000 Years? London: Routledge.
Fuller, D. Q. 2011. Pathways to Asian Civilizations: Tracing the Origins and Spread of Rice and Rice Cultures. Rice 4 (3–4): 78–92.
Grinin, L. E. 2006. Periodization of History: A Theoretic-Mathematical Analysis. In Grinin, L. E., de Munck, V., and Korotayev, A. V. (eds.), History & Mathematics: Analyzing and Modeling Global Development (pp. 10–38). Moscow: KomKniga.
Grinin, L. E. 2007. Production Revolutions and the Periodization of History. Herald of the Russian Academy of Sciences 77 (2): 150–156.
Gross, B. L., and Zhao, Z. 2014. Archaeological and Genetic Insights into the Origins of Domesticated Rice. Proceedings of the National Academy of Sciences 111 (17): 6190–6197.
Grossman, G., and Helpman, E. 1991. Innovation and Growth in the Global Economy. Cambridge, MA: MIT Press.
Hanks, B., and Doonan, R. 2009. From Scale to Practice: A New Agenda for the Study of Early Metallurgy on the Eurasian Steppe. Journal of World Prehistory 22 (4): 329–356.
Headrick, D. R. 2009. Technology: A World History. New York: Oxford University Press.
Higham, C., Higham, T., Ciarla, R., Douka, K., Kijngam, A., and Rispoli, F. 2011. The Origins of the Bronze Age of Southeast Asia. Journal of World Prehistory 24 (4): 227–274.
Hillman, G. C. 2001. New Evidence of Lateglacial Cereal Cultivation at Abu Hureyra on the Euphrates. Holocene 11: 383–393.
Hoerner, S. J. von. 1975. Population Explosion and Interstellar Expansion. Journal of the British Interplanetary Society 28: 691–712.
Huang, X., Kurata, N., Wei, X., Wang, Z. X., Wang, A., Zhao, Q., ... and Han, B. 2012. A Map of Rice Genome Variation Reveals the Origin of Cultivated Rice. Nature 490 (7421): 497–501.
Hudyakov, Yu. S. 2002. War Chariots in Southern Siberia and Central Asia. Northern Asia during Bronze Era: Space, Time, Culture (pp. 139–141). Barnaul: Izdatel'stvo AGU. In Russian (Худяков Ю. С. Боевые колесницы в Южной Сибири и Центральной Азии. Северная Азия в эпоху бронзы: пространство, время, культура, c. 139–141. Барнаул: Издательство АГУ).
Johansen, A., and Sornette, D. 2001. Finite-time Singularity in the Dynamics of the World Population and Economic Indices. Physica A 294 (3–4): 465–502.
Jones, Ch. I. 1995. R & D-Based Models of Economic Growth. The Journal of Political Economy 103: 759–784.
Jones, Ch. I. 2003. Population and Ideas: A Theory of Endogenous Growth. In Aghion, P., Frydman, R., Stiglitz, J., and Woodford, M. (eds.), Knowledge, Information, and Expectations in Modern Macroeconomics: In Honor of Edmund S. Phelps (pp. 498–521). Princeton, NJ: Princeton University Press.
Jones, Ch. I. 2005. The Shape of Production Functions and the Direction of Technical Change. The Quarterly Journal of Economics 120: 517–549.
Jones, G., Charles, M. P., Jones, M. K., Colledge, S., Leigh, F. J., Lister, D. A., ... and Jones, H. 2013. DNA Evidence for Multiple Introductions of Barley into Europe Following Dispersed Domestications in Western Asia. Antiquity 87 (337): 701–713.
Kapitza, S. P. 1992. The Mathematical Model of World Population Growth. Matematicheskoe modelirovanie 4 (6): 65–79. In Russian (Капица С. П. Математическая модель роста народонаселения мира. Математическое моделирование 4 (6): 65–79).
Kapitza, S. P. 1999. How Many People Lived, Lives and will Live on the Earth. Moscow: Nauka. In Russian (Капица С. П. Сколько людей жило, живет и будет жить на Земле. М.: Наука).
Killick, D., and Fenn, T. 2012. Archaeometallurgy: The Study of Preindustrial Mining and Metallurgy. Annual Review of Anthropology 41: 559–575.
Knyazeva, E. N., and Kurdjumov, S. P. 2005. The Basics of Synergetics. Moscow: URSS. In Russian (Князева Е. Н., Курдюмов С. П. Основы синергетики. М.: УРСС).
Komlos, J., and Nefedov, S. 2002. A Compact Macromodel of Pre-Industrial Population Growth. Historical Methods 35: 92–94.
Korotayev, A. 2005. A Сompact Macromodel of World System Evolution. Journal of World-Systems Research 11 (1): 79–93.
Korotayev, A. V. 2006. The World System History Periodization and Mathematical Models of Socio-Historical Processes. In Grinin, L., de Munck, V., and Korotayev, A. (eds.), History and Mathematics: Analyzing and Modeling Global Development (pp. 39–98). Moscow: KomKniga/URSS.
Korotayev, A. 2007. Compact Mathematical Models of World System Development, and How They Can Help us to Clarify our Understanding of Globalization Processes. In Modelski, G., Devezas, T., and Thompson, W. R. (eds.), Globalization as Evolutionary Process: Modeling Global Change (pp. 133–160). London: Routledge.
Korotayev, A. 2008. Globalization and Mathematical Modeling of Global Development. In Grinin, L. E., Beliaev, D. D., and Korotayev, A. V. (eds.), Hierarchy and Power in the History of Civilizations: Political Aspects of Modernity (pp. 225–240). Moscow: LIBROCOM/URSS.
Korotayev, A. 2012. Globalization and Mathematical Modeling of Global Development. In Grinin, L., Ilyin, I., and Korotayev, A. (eds.), Globalistics and Globalization Studies (pp. 148–158). Volgograd: Uchitel Publishing House.
Korotayev, A., Khaltourina, D. 2006. Introduction to Social Macrodynamics: Secular Cycles and Millennial Trends in Africa. Moscow: KomKniga/URSS.
Korotayev, A., Malkov, A., and Khaltourina, D. 2006a. Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth. Moscow: KomKniga/URSS.
Korotayev, A., Malkov, A., Khaltourina, D. 2006b. Introduction to Social Macrodynamics: Secular Cycles and Millennial Trends. Moscow: KomKniga/URSS.
Korotayev, A., Malkov, A. 2016. A Compact Mathematical Model of the World System Economic and Demographic Growth, 1 CE – 1973 CE. International Journal of Mathematical Models and Methods in Applied Sciences 10: 200–209.
Kremer, M. 1993. Population Growth and Technological Change: One Million B.C. to 1990. The Quarterly Journal of Economics 108: 681–716.
Kurdjumov, S. P. 1999. Regimes with Sharpening. The Evolution of Idea: The Laws of Coevolution of Complex Structures. Moscow: Nauka. In Russian (Курдюмов С. П. Режимы с усилением. Эволюция идеи: Законы коэволюции сложных обществ. М.: Наука).
Kuzmin, Yu. V. 2013. Two Trajectories in the Neolithization of Eurasia: Pottery versus Agriculture (Spatiotemporal Patterns). Radiocarbon 55 (2–3): 1304–1313.
Kuznets, S. 1960. Population Change and Aggregate Output. In Becker, G. S. (ed.), Demographic and Economic Change in Developed Countries (pp. 324–340). Princeton, NJ: Princeton University Press.
Larson, G., Albarella, U., Dobney, K., Rowley-Conwy, P., Schibler, J., Tresset, A., ... and Bălăçsescu, A. 2007. Ancient DNA, Pig Domestication, and the Spread of the Neolithic into Europe. Proceedings of the National Academy of Sciences 104 (39): 15276–15281.
Larson, G., Liu, R., Zhao, X., Yuan, J., Fuller, D., Barton, L., ... and Luo, Y. 2010. Patterns of East Asian Pig Domestication, Migration, and Turnover Revealed by Modern and Ancient DNA. Proceedings of the National Academy of Sciences 107 (17): 7686–7691.
Lee, R. D. 1986. Malthus and Boserup: A Dynamic Synthesis. In Coleman, D., and Schofield, R. (eds.), The State of Population Theory: Forward from Malthus (pp. 96–130). Oxford: Blackwell.
Li, X., Shang, X., Dodson, J., and Zhou, X. 2009. Holocene Agriculture in the Guanzhong Basin in NW China Indicated by Pollen and Charcoal Evidence. The Holocene 19 (8): 1213–1220.
Li, Z. M., Zheng, X. M., and Ge, S. 2011. Genetic Diversity and Domestication History of African Rice (Oryza glaberrima) as Inferred from Multiple Gene Sequences. Theoretical and Applied Genetics 123 (1): 21–31.
Linduff, K. M., and Mei, J. 2009. Metallurgy in Ancient Eastern Asia: Retrospect and Prospects. Journal of World Prehistory 22 (3): 265–281.
Liu, L., Lee, G. A., Jiang, L., and Zhang, J. 2007. Evidence for the Early Beginning (c. 9000 cal. BP) of Rice Domestication in China: a Response. The Holocene 17 (8): 1059–1068.
Malthus, T. 1978 [1798]. Population: The First Essay. Ann Arbor, MI: University of Michigan Press.
McEvedy, C., and Jones, R. 1978. Atlas of World Population History. New York: Facts on File.
Modelski, G. 2000. World System Evolution. In Denemark, R. A., Friedman, J., Gills, B. K., and Modelski, G. (eds.), World System History: The Social Science of Long-term Change (pp. 24–53). London: Routledge.
Modelski, G. 2003. World Cities: –3000 to 2000. Washington, DC: FAROS 2000.
Molina, J., Sikora, M., Garud, N., Flowers, J. M., Rubinstein, S., Reynolds, A., ... and Purugganan, M. D. 2011. Molecular Evidence for a Single Evolutionary Origin of Domesticated Rice. Proceedings of the National Academy of Sciences 108 (20): 8351–8356.
Moorey, P. R. S. 1986. The Emergence of the Light, Horse‐drawn Chariot in the Near‐East c. 2000–1500 B.C. World Archaeology 18 (2): 196–215.
Morrell, P. L., and Clegg, M. T. 2007. Genetic Evidence for a Second Domestication of Barley (Hordeum vulgare) East of the Fertile Crescent. Proceedings of the National Academy of Sciences 104 (9): 3289–3294.
Naderi, S., Rezaei, H. R., Pompanon, F., Blum, M. G., Negrini, R., Naghash, H. R., ... and Taberlet, P. 2008. The Goat Domestication Process Inferred from Large-scale Mitochondrial DNA Analysis of Wild and Domestic Individuals. Proceedings of the National Academy of Sciences 105 (46): 17659–17664.
Ohnishi, O. 1998. Search for the Wild Ancestor of Buckwheat III. The Wild Ancestor of Cultivated Common Buckwheat, and of Tatary Buckwheat. Economic Botany 52 (2): 123–133.
Peregrine, P. 2003. Atlas of Cultural Evolution. World Cultures 14: 2–88.
Peregrine, P., and Ember, M. 2001. (Eds.) Encyclopedia of Prehistory. 9 vols. New York: Kluwer.
Perrier, X., De Langhe, E., Donohue, M., Lentfer, C., Vrydaghs, L., Bakry, F., ... and Denham, T. 2011. Multidisciplinary Perspectives on Banana (Musa spp.) Domestication. Proceedings of the National Academy of Sciences 108 (28): 11311–11318.
Podlazov, A. V. 2000. Theoretical Demography as the Basis of Mathematical History. Moscow: IPM RAN. In Russian (Подлазов А. В. Теоретическая демография как основа математической истории. М.: ИПМ РАН).
Podlazov, A. V. 2001. The Basic Equation of Theoretical Demography and the Model of Global Demographic Transition. Moscow: IPM RAN. In Russian (Подлазов А. В. Основное уравнение теоретической демографии и модель глобального демографического перехода. М.: ИПМ РАН).
Podlazov, A. V. 2002. Theoretical Demography. Models of Population Growth and Global Demographic Transition. In Malinetski, G. G., and Kurdjumov, S. P. (eds.), A New Development in Complexity Studies. The View into the 3rd Millennium (pp. 324–345). Moscow: Nauka. In Russian (Подлазов А. В. Теоретическая демография. Модели роста народонаселения и глобального демографического перехода. Новое развитие в изучении сложных систем. Взгляд в 3-е тысячелетие / ред. Г. Г. Малинецкий, С. П. Курдюмов, с. 324–345. М.: Наука).
Podlazov, A. V. 2004. Theory of the Global Demographic Process. In Dmitriev, M. G., and Petrov, A. P. (eds.), Mathematical Modeling of Social and Economic Dynamics (pp. 269–272). Moscow: Russian State Social University.
Price, T. D., and Bar-Yosef, O. 2011. The Origins of Agriculture: New Data, New Ideas. Current Anthropology 52 (S4): S163–S174.
Radivojević, M., Rehren, T., Kuzmanović-Cvetković, J., Jovanović, M., and Northover, J. P. 2013. Tainted Ores and the Rise of Tin Bronzes in Eurasia, c. 6500 Years Ago. Antiquity 87 (338): 1030–1045.
Radivojević, M., Rehren, T., Pernicka, E., Šljivar, D., Brauns, M., and Borić, D. 2010. On the Origins of Extractive Metallurgy: New Evidence from Europe. Journal of Archaeological Science 37 (11): 2775–2787.
Ren, X., Nevo, E., Sun, D., and Sun, G. 2013. Tibet as a Potential Domestication Center of Cultivated Barley of China. Plos ONE 8: e62700.
Roberts, B. W., Thornton, C. P., and Pigott, V. C. 2009. Development of Metallurgy in Eurasia. Antiquity 83 (322): 1012–1022.
Roullier, C., Duputié, A., Wennekes, P., Benoit, L., Fernandez Bringas, V. M., et al. 2013. Disentangling the Origins of Cultivated Sweet Potato (Ipomoea batatas (L.) Lam.). PLoS ONE 8 (5): e62707.
Saisho, D., and Purugganan, M. D. 2007. Molecular Phylogeography of Domesticated Barley Traces Expansion of Agriculture in the Old World. Genetics 177 (3): 1765–1776.
Shaughnessy, E. L. 1988. Historical Perspectives on the Introduction of the Chariot into China. Harvard Journal of Asiatic Studies 48 (1): 189–237.
Shishkov, U. V. 2005. The Demographic Adventures of a Physicist. Obschestvennye nauki i sovremennost 2: 155–164. In Russian (Шишков Ю. В. Демографические похождения физика. Общественные науки и современность 2: 155–164).
Simon, J. 1977. The Economics of Population Growth. Princeton, NJ: Princeton University Press.
Simon, J. 1981. The Ultimate Resource. Princeton, NJ: Princeton University Press.
Simon, J. 2000. The Great Breakthrough and its Cause. Ann Arbor, MI: University of Michigan Press.
Taagepera, R. 1976. Crisis around 2005 A.D.? A Technology-Population Interaction Model. General Systems 21: 137–138.
Taagepera, R. 1979. People, Skills, and Resources: An Interaction Model for World Population Growth. Technological Forecasting and Social Change 13: 13–30.
Taagepera, R. 2014. A World Population Growth Model: Interaction with Earth's Carrying Capacity and Technology in Limited Space. Technological Forecasting and Social Change 82: 34–41.
Thornton, C. P. 2009. The Emergence of Complex Metallurgy on the Iranian Plateau: Escaping the Levantine Paradigm. Journal of World Prehistory 22 (3): 301–327.
Tsirel, S. V. 2004. On the Possible Reasons for the Hyperexponential Growth of the Earth Population. In Dmitriev, M. G., and Petrov, A. P. (eds.), Mathematical Modeling of Social and Economic Dynamics (pp. 367–369). Moscow: Russian State Social University.
Turchin, P. 2003. Historical Dynamics: Why States Rise and Fall. Princeton, NJ: Princeton University Press.
Tylecote, R. F. 1976. A history of Metallurgy. London: Institute of Materials.
Vaughan, D. A., Lu, B. R., and Tomooka, N. 2008. The Evolving Story of Rice Evolution. Plant Science 174 (4): 394–408.
Wallerstein, I. 1974. The Modern World-System. Vol. 1: Capitalist Agriculture and the Origins of the European World-Economy in the Sixteenth Century. New York: Academic Press.
Wallerstein, I. 1987. World-Systems Analysis. In Giddens, A., and Turner, J. (eds.), Social Theory Today (pp. 309–324). Cambridge: Polity Press.
Wallerstein, I. 2004. World-Systems Analysis: An Introduction. Durham, NC: Duke University Press.
Yang, X., Wan, Z., Perry, L., Lu, H., Wang, Q., Zhao, C., ... and Ge, Q. 2012. Early Millet Use in Northern China. Proceedings of the National Academy of Sciences 109 (10): 3726–3730.
Zeder, M.A. 2011. The Origins of Agriculture in the Near East. Current Anthropology 52 (S4): 221–235.
Zeder, M. A., and Hesse, B. 2000. The Initial Domestication of Goats (Capra hircus) in the Zagros Mountains 10,000 Years Ago. Science 287 (5461): 2254–2257.
Zohary, D., and Hopf, M. 2000. Domestication of Plants in the Old World. Oxford: Oxford University Press.





